All SAT II Math II Resources
Example Questions
Example Question #3 : Linear Functions
The angles containing the variable all reside along one line, therefore, their sum must be .
Because and are opposite angles, they must be equal.
Example Question #1 : Finding Angles
What angle do the minute and hour hands of a clock form at 6:15?
There are twelve numbers on a clock; from one to the next, a hand rotates . At 6:15, the minute hand is exactly on the "3" - that is, on the position. The hour hand is one-fourth of the way from the "6" to the "7" - that is, on the position. Therefore, the difference is the angle they make:
.
Example Question #2 : Finding Angles
In triangle , and . Which of the following describes the triangle?
None of the other responses is correct.
is acute and scalene.
is acute and isosceles.
is obtuse and scalene.
is obtuse and isosceles.
is acute and isosceles.
Since the measures of the three interior angles of a triangle must total ,
All three angles have measure less than , making the triangle acute. Also, by the Isosceles Triangle Theorem, since , ; the triangle has two congruent sides and is isosceles.
Example Question #3 : Finding Angles
In , and are complementary, and . Which of the following is true of ?
None of the other responses is correct.
is acute and scalene.
is acute and isosceles.
is right and scalene.
is right and isosceles.
is right and scalene.
and are complementary, so, by definition, .
Since the measures of the three interior angles of a triangle must total ,
is a right angle, so is a right triangle.
and must be acute, so neither is congruent to ; also, and are not congruent to each other. Therefore, all three angles have different measure. Consequently, all three sides have different measure, and is scalene.
Example Question #4 : Finding Angles

The above figure is a regular decagon. Evaluate .
As an interior angle of a regular decagon, measures
.
Since and are two sides of a regular polygon, they are congruent. Therefore, by the Isosceles Triangle Theorem,
The sum of the measures of a triangle is , so
Example Question #5 : Finding Angles

The above hexagon is regular. What is ?
None of the other responses is correct.
Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures
.
The four angles of the quadrilateral are . Their sum is , so we can set up, and solve for in, the equation:
Example Question #61 : 2 Dimensional Geometry
What angle do the minute and hour hands of a clock form at 4:15?
There are twelve numbers on a clock; from one to the next, a hand rotates . At 4:15, the minute hand is exactly on the "3" - that is, on the position. The hour hand is one-fourth of the way from the "4" to the "5" - that is, on the position. Therefore, the difference is the angle they make:
.
Example Question #62 : 2 Dimensional Geometry
If the vertical angles of intersecting lines are: and , what must be the value of ?
Vertical angles of intersecting lines are always equal.
Set the two expressions equal to each other and solve for .
Subtract from both sides.
Subtract 6 from both sides.
The answer is:
Example Question #63 : 2 Dimensional Geometry
If the angles in degrees are and which are complementary to each other, what is three times the value of the smallest angle?
Complementary angles add up to 90 degrees.
Set up an equation such that the sum of both angles equal to 90.
Subtract 10 from both sides.
Divide by 2 on both sides.
The angles are:
Three times the value of the smallest angle is:
The answer is:
Example Question #64 : 2 Dimensional Geometry
If the angles and are supplementary, what must be the value of ?
Supplementary angles sum up to 180 degrees.
Add five on both sides.
Divide by negative five on both sides to determine .
The answer is:
All SAT II Math II Resources




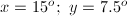




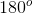
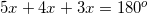



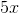



























































![m \angle B = \left [\frac{180(10-2)}{10} \right ] ^{\circ }= 144^{\circ }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/217578/gif.latex)















































































