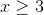Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Single-Variable Algebra

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #101 : Single Variable Algebra

Give the set of all real solutions of the equation $8 x -2 x ^{\frac{1}{2}} - 3 = 0$ .

Possible Answers:

$\left \{ \frac{1}{4} , \frac{9}{16} \right \}$

$\left \{ - \frac{9}{16} , \frac{9}{16} \right \}$

$\left \{ - \frac{1}{4} , \frac{1}{4} \right \}$

$\left \{ - \frac{1}{4} , \frac{9}{16} \right \}$

None of these

Correct answer:

None of these

Explanation:

Set $y = x^{\frac{1}{2}}$ . Then $x = \left (x^{\frac{1}{2}} \right )^{2} = y ^{2}$ .

$8 x -2 x ^{\frac{1}{2}} - 3 = 0$ can be rewritten as

$8 \left (x^{\frac{1}{2}} \right )^{2} -2 x ^{\frac{1}{2}} - 3 = 0$

Substituting $y^{2}$ for and for $x^{\frac{1}{2}}$ , the equation becomes

$8y^{2} -2 y - 3 = 0$ ,

a quadratic equation in .

This can be solved using the method. We are looking for two integers whose sum is and whose product is 8 (-3) = -24 . Through some trial and error, the integers are found to be and 4, so the above equation can be rewritten, and solved using grouping, as

$8y^{2}-6y + 4 y - 3 = 0$

2y ( 4 y - 3)+1 ( 4 y - 3) = 0

(2y +1) ( 4 y - 3) = 0

By the Zero Product Principle, one of these factors is equal to zero:

Either:

2y + 1 = 0

2y + 1 - 1 = 0 - 1

2y = - 1

$\frac{2y}{2} = \frac{- 1}{2}$

$y = - \frac{1}{2}$

Substituting back:

$x^{\frac{1}{2}} = -\frac{1}{2}$ , or $\sqrt{x} = - \frac{1}{2}$

However, this does not hold for any real value of . No solution is yielded here.

Or:

4y - 3 = 0

4y - 3+ 3 = 0+ 3

4 y = 3

$\frac{4 y}{4} = \frac{3}{4}$

$y= \frac{3}{4}$

Substituting back:

$x^{\frac{1}{2}} = \frac{3}{4}$ , or $\sqrt{x} = \frac{3}{4}$

$(\sqrt{x} )^{2} = \left (\frac{3}{4} \right )^{2}$

$x = \frac{9}{16}$ ,

the only solution. This is not among the choices.

Report an Error

Example Question #1 : Solving Inequalities

Give the solution set of the inequality

$\frac{2x-5}{x-7} > 0$

Possible Answers:

$\left ( 2\frac{1}{2}, 7 \right )$

$\left ( 2\frac{1}{2}, 7 \right )\cup \left ( 7, \infty\right )$

$\left (-\infty, 2\frac{1}{2} \right )$

$\left (-\infty, 2\frac{1}{2} \right ) \cup \left ( 7, \infty\right )$

$\left (-\infty, 2\frac{1}{2} \right ) \cup \left ( 2\frac{1}{2}, 7 \right ) \cup \left ( 7, \infty\right )$

Correct answer:

$\left (-\infty, 2\frac{1}{2} \right ) \cup \left ( 7, \infty\right )$

Explanation:

Two numbers of like sign have a positive quotient.

Therefore, $\frac{2x-5}{x-7} > 0$ has as its solution set the set of points at which 2x-5 and x- 7 are both positive or both negative.

To find this set of points, we identify the zeroes of both expressions.

2x- 5 = 0

2x= 5

$x = 2\frac{1}{2}$

x-7 = 0

x = 7

Since $\frac{2x-5}{x-7}$ is nonzero we have to exclude $x = 2\frac{1}{2}$ ; x = 7 is excluded anyway since it would bring about a denominator of zero. We choose one test point on each of the three intervals $\left (-\infty, 2\frac{1}{2} \right ) , \left ( 2\frac{1}{2}, 7 \right ) , \left ( 7, \infty\right )$ and determine where the inequality is correct.

$\left (-\infty, 2\frac{1}{2} \right )$

Choose x = 0 :

$\frac{2 \cdot 0-5}{0-7} = \frac{-5}{-7} = \frac{5}{7} > 0$ - True.

$\left ( 2\frac{1}{2}, 7 \right )$

Choose x=3 :

$\frac{2 \cdot 3-5}{3-7} = \frac{6}{-4} =- \frac{3}{2} > 0$ - False.

$\left ( 7, \infty\right )$

Choose x = 8 :

$\frac{2 \cdot 8-5}{8-7} = \frac{11}{1} =11> 0$ - True.

The solution set is $\left (-\infty, 2\frac{1}{2} \right ) \cup \left ( 7, \infty\right )$

Report an Error

Example Question #1 : Solving Inequalities

Solve for x.

$2x-7\geq 1$

Possible Answers:

$x\geq 5$

x> 4

$x\geq 4$

$x\geq -3$

$x\leq 4$

Correct answer:

$x\geq 4$

Explanation:

Solving inequalities is very similar to solving an equation. We must start by isolating x by moving the terms farthest from it to the other side of the inequality. In this case, add 7 to each side.

$2x-7+7\geq 1+7$

$2x\geq 8$

Now, divide both sides by 2.

$x\geq 4$

Report an Error

Example Question #1 : Solving Inequalities

Solve for x.

$3x+2\geq -7$

Possible Answers:

$x\geq -3$

$x\leq -3$

$x\geq 1$

$x\geq 3$

$x\geq -1$

Correct answer:

$x\geq -3$

Explanation:

Solving inequalities is very similar to solving an equation. We must start by isolating x by moving the terms farthest from it to the other side of the inequality. In this case, subtract 2from each side.

$3x+2-2\geq -7-2$

$3x\geq -9$

Now, divide both sides by 2.

$x\geq -3$

Report an Error

Example Question #1 : Solving Inequalities

Solve the following inequality:

3x+7<9

Possible Answers:

x<-4

x< 9

x<7

x<3

$x< \frac{2}{3}$

Correct answer:

$x< \frac{2}{3}$

Explanation:

To solve for an inequality, you solve like you would for a single variable expression and get by itself.

First, subtract from both sides to get,

3x<2 .

Then divide both sides by and your final answer will be,

$x< \frac{2}{3}$ .

Report an Error

Example Question #5 : Solving Inequalities

Solve the inequality: 3-(3-2x)<10

Possible Answers:

$x>-\frac{1}{5}$

x>5

$x<\frac{1}{5}$

x<5

x<-5

Correct answer:

x<5

Explanation:

Simplify the left side.

3-3+2x<10

The inequality becomes:

2x<10

Divide by two on both sides.

$\frac{2}{2}x<\frac{10}{2}$

The answer is: x<5

Report an Error

Example Question #4 : Solving Inequalities

Solve the inequality: $2x+6\leq 9x-3$

Possible Answers:

$x\geq-\frac{3}{11}$

$x\geq-\frac{9}{7}$

$x\geq\frac{9}{7}$

$x\leq-\frac{9}{7}$

$x\leq-\frac{3}{11}$

Correct answer:

$x\geq\frac{9}{7}$

Explanation:

Subtract on both sides.

$2x+6-2x\leq 9x-3-2x$

$6\leq 7x-3$

Add 3 on both sides.

$6+3\leq 7x-3+3$

$9\leq 7x$

Divide by 7 on both sides.

$\frac{9}{7}\leq \frac{7x}{7}$

$\frac{9}{7}\leq x$

The answer is: $x\geq\frac{9}{7}$

Report an Error

Example Question #1 : Simplifying Expressions

Simplify the expression.

$\small \frac{(x^2y^2)(x^3y^4z)}{x^4y^3z^4}$

Possible Answers:

$\small \frac{x^2y^5}{z^3}$

$\small \frac{xy^3}{z^3}$

$\small \frac{z^3}{x^2y^5}$

$\small \frac{z^3}{xy^3}$

Correct answer:

$\small \frac{xy^3}{z^3}$

Explanation:

$\small \frac{(x^2y^2)(x^3y^4z)}{x^4y^3z^4}$

Because we are only multiplying terms in the numerator, we can disregard the parentheses.

$\small \frac{(x^2y^2)(x^3y^4z)}{x^4y^3z^4}=\frac{x^2y^2x^3y^4z}{x^4y^3z^4}$

To combine like terms in the numerator, we add their exponents.

$\small \frac{x^5y^6z}{x^4y^3z^4}$

To combine like terms between the numerator and denominator, subtract the denominator exponent from the numerator exponent.

$x^{5-4}y^{6-3}z^{1-4}=xy^3z^{-3}$

Remember that any negative exponents stay in the denominator.

$\frac{xy^3}{z^3}$

Report an Error

Example Question #1 : Simplifying Expressions

Give the value of that makes the polynomial $9x^{2}+ Nx + 100$ the square of a linear binomial.

Possible Answers:

None of the other responses gives a correct answer.

N = 60

N = 30

N = 90

N = 81

Correct answer:

N = 60

Explanation:

A quadratic trinomial is a perfect square if and only if takes the form

$A^{2} \pm 2AB + B^{2}$ for some values of and .

$9x^{2}+ Nx + 100 = (3x)^{2} + Nx + 10^{2}$ , so

A = 3x and B = 10 .

For $9x^{2}+ Nx + 100$ to be a perfect square, it must hold that

$Nx = 2AB = 2 \cdot 3x \cdot 10 = 60x$ ,

so N = 60 . This is the correct choice.

Report an Error

Example Question #3 : Simplifying Expressions

Factor:

$27Q^{3}- 270Q^{2}+900Q -1,000$

Possible Answers:

$(3Q-10)(9Q^{2}- 30 Q +100)$

The polynomial is prime.

$(3Q-10)(3Q+10)^{2}$

$(3Q - 10)^{3}$

$(3Q-10)(9Q^{2}+ 30 Q +100)$

Correct answer:

$(3Q - 10)^{3}$

Explanation:

$27Q^{3}- 270Q^{2}+900Q -1,000$

$=\left (3Q \right )^{3}- 3 \cdot 90Q^{2}+3\cdot 300Q -10^{3}$

$=\left (3Q \right )^{3}- 3 \cdot 9Q^{2}\cdot 10+3\cdot 3Q \cdot 10^{2} -10^{3}$

$=\left (3Q \right )^{3}- 3 \cdot \left (3Q \right )^{2}\cdot 10+3\cdot 3Q \cdot 10^{2} -10^{3}$

This can be factored out as the cube of a difference, where A = 3Q, B = 10 :

$A^{3}- 3A^{2}B+3AB^{2} -B^{3} = (A - B)^{3}$

Therefore,

$27Q^{3}- 270Q^{2}+900Q -1,000$

$=\left (3Q \right )^{3}- 3 \cdot \left (3Q \right )^{2}\cdot 10+3\cdot 3Q \cdot 10^{2} -10^{3}$

$= (3Q - 10)^{3}$

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Kaitlyn
Certified Tutor

Fairfield University, Bachelor of Science, Biology, General. NUI Galway Ireland, Master of Science, Neuroscience.

View SAT Subject Test in Mathematics Level 1 Tutors

Amanda
Certified Tutor

Seattle University, Current Undergrad Student, Applied Mathematics.

View SAT Subject Test in Mathematics Level 1 Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Boston, GRE Tutors in Houston, Physics Tutors in San Diego, SSAT Tutors in New York City, SSAT Tutors in Dallas Fort Worth, Statistics Tutors in Miami, LSAT Tutors in Phoenix, Statistics Tutors in Phoenix, Algebra Tutors in Philadelphia, English Tutors in Dallas Fort Worth

Popular Courses & Classes

ISEE Courses & Classes in Philadelphia, Spanish Courses & Classes in Miami, ACT Courses & Classes in San Diego, SAT Courses & Classes in Houston, LSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Chicago, ISEE Courses & Classes in Atlanta, GMAT Courses & Classes in Seattle, GMAT Courses & Classes in Philadelphia

Popular Test Prep

GMAT Test Prep in Atlanta, GMAT Test Prep in Houston, ISEE Test Prep in Philadelphia, GMAT Test Prep in Philadelphia, ISEE Test Prep in Miami, MCAT Test Prep in Chicago, MCAT Test Prep in Denver, ACT Test Prep in San Diego, GMAT Test Prep in Denver, ACT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Single-Variable Algebra

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #101 : Single Variable Algebra

Example Question #1 : Solving Inequalities

Example Question #1 : Solving Inequalities

Example Question #1 : Solving Inequalities

Example Question #1 : Solving Inequalities

Example Question #5 : Solving Inequalities

Example Question #4 : Solving Inequalities

Example Question #1 : Simplifying Expressions

Example Question #1 : Simplifying Expressions

Example Question #3 : Simplifying Expressions

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: