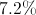Inverse variation takes the form:

Plugging in:

Then solve when x=3:

For an indirect proportionality, use the equation

If rate of speed is indirectly proportional to the time, then the speed is y (3 miles per hour) and the time is x (4 hours).

Replace those into the indirect proportionality formula

Solve for k by multiplying by 4 on both sides

The person traveled 12 miles.

Rewrite the two equations by setting  and  and substituting:

In terms of  and , this is the system of linear equations:

Solve the first equation for :

Substitute this expression for  in the second equation, then simplify:

The statement is identically false. Therefore, the original system cannot have a solution.

The system has no solution. The clue can be seen in the second equation 

.

The square root of a number (assuming it is real) must be a nonnegative number. Consequently, by the closure of the nonnegative numbers under multiplication, it holds that  and  are nonnegative as well. Also, by the closure of the nonnegative numbers under multiplication,  must also be a positive quantity. Therefore, 

cannot have a solution; consequently, neither can the system.

Rewrite the two equations by setting  and  and substituting:

In terms of  and , this is a two-by-two linear system: 

Rewrite this as an augmented matrix as follows:

Perform the following row operations to make the left two columns the identity matrix :

 and .

Substituting  back for :

Taking the reciprocal of both sides:

.

Rewrite the two equations by setting  and  and substituting:

In terms of  and , this is the system of linear equations:

Rewrite this as an augmented matrix as follows:

Perform the following row operations to make the left two columns the identity matrix :

 and .

Setting  and solving for  by cubing both sides:

Let  be a cube root of 64. The question is to find a solution of the equation

.

One way to solve this is to subtract 64 from both sides:

64 is a perfect cube, so, as the difference of cubes, the left expression can be factored:

We can set both factors equal to zero and solve:

4 is a cube root of 64; however, this is not one of the choices.

Setting 

,

we can make use of the quadratic formula, setting  in the following:

 and  are the other two cube roots of ; neither is a choice. Therefore, none of the four choices given are cube roots.

How to calculate the amount of sales tax?

1.      Convert tax percentage into a decimal by moving the decimal point two spaces to the left.
2.      Multiple the pre-tax value by the newly calculated decimal value in order to find the cost of the sales tax.
3.      Add the sales tax value to the pre-tax value to calculate the total cost.

Calculating sales tax at time of purchase:

In order to calculate the sales tax of an item, we need to first multiply the pre-tax cost of the item by the sales tax percentage after it has been converted into a decimal. Once the sales tax has been calculated it needs to be added to the pre-tax value in order to find the total cost of the item. Let's start by working with an example. If a magazine costs $2.35 and has a 6% sales tax, then what is the total cost of the item. First, we need to convert the sales tax percentage into a decimal by moving the point two spaces to the left.

Now, we need to multiply the pre-tax cost of this item by this value in order to calculate the sales tax cost.

Round to two decimal places since our total is in dollars and cents.

Last, add this value to the pre-tax value of the item to find the total cost.

Calculating the sales tax percentage of a total:

If we are given the total cost of an item or group of items and the pre-tax cost of the good(s), then we can calculate the sales tax percentage of the total cost. First, we need to subtract the pre-tax value from the total cost of the purchase. Next, we need to create a ratio of the sales tax to the pre-tax cost off the items. Last, we need to create a proportion where the pre-tax cost is related to 100% and solve for the percentage of the sales tax. Let's start by working through an example. If a person pays $245.64 for groceries that cost $220.00 pre tax, then what is the sales tax percentage for the items.

First, subtract the pre-tax value from the total cost of the items to find the sales tax cost.

Next, create a ratio of the sales tax to the pre-tax cost of the items.

Last, create a proportion where the pre-tax value is proportional to 100% and solve for the percentage of sales tax.

Cross multiply and solve.

Isolate the sales tax percentage to the left side of the equation by dividing each side by the pre-tax value.

Round to two decimal places since our answer is in dollars and cents.

Last, we can check this answer by calculating the sales tax percentage of the total as seen previously.

First, we need to convert the sales tax percentage into a decimal by moving the point two spaces to the left.

Now, we need to multiply the pre-tax cost of this item by this value in order to calculate the sales tax cost.

Round to two decimal places since our total is in dollars and cents.

Last, add this value to the pre-tax value of the item to find the total cost.

Our answers check out; therefore they are correct. Now, let's use this information to solve the given problem.

Solution: 

If each soda cost $1.56 and Jane bought four, the total for the sodas was:

And she paid $6.93

The sales tax was 11%.

 is the cube of , which is the difference of twelve and a number. Therefore,  is "the cube of the difference of twelve and a number."

This question involves muliple steps to attain the correct answer.

To solve for the weight of the bucket (we will let 'x' represent this) the following equation can be set up:

To isolate x, subtract 9 * 1.22 (which is equal to 10.98) from both sides. We find x to be equal to 2.32.

The question asks us for the percentage of the total weight, so to find this, we must divide 2.32 by the total weight and multiple our answer by 100.

Rounded to two decimal points of accuracy, the final answer is 17.44%.