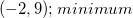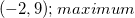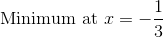Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Properties of Functions and Graphs

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #41 : Properties Of Functions And Graphs

What is the slope of the following equation? 2y = 3-7x

Possible Answers:

$\frac{3}{2}$

$-\frac{7}{2}$

Correct answer:

$-\frac{7}{2}$

Explanation:

The given equation will need to be rewritten in slope intercept format.

y=mx+b

Divide by two on both sides.

$\frac{2y }{2}=\frac{ 3-7x}{2}$

Rearrange the right side by order of powers.

$y= -\frac{7}{2}x+\frac{3}{2}$

The slope can be seen as $-\frac{7}{2}$

The answer is: $-\frac{7}{2}$

Report an Error

Example Question #41 : Functions And Graphs

What is the slope of the given equation? $y=-\frac{1}{2x}+3$

Possible Answers:

$\textup{The slope does not exist.}$

$-\frac{1}{2}$

Correct answer:

$\textup{The slope does not exist.}$

Explanation:

The slope in a linear equation is defined as y=mx+b .

The x-variable exists in the denominator, which refers to the parent function of:

$y=\frac{1}{x}$

This function is not linear, and will have changing slope along its domain.

The answer is: $\textup{The slope does not exist.}$

Report an Error

Example Question #1 : Maximum And Minimum

What is the vertex of the following function? Is it a maximum or a minimum?

$\small f(x) = -3(x-2)^2+9$

Possible Answers:

$\small (-2,9); minimum$

$\small (2,9); minimum$

$\small (-2,9); maximum$

$\small \small (2,9); maximum$

$\small (2,-9); maximum$

Correct answer:

$\small \small (2,9); maximum$

Explanation:

The equation of a parabola can be written in vertex form

$\small f(x) = a(x-h)^2+k$

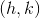
where $\small \tiny (h,k)$ is the vertex and $\tiny a$ determines if it is a minimum or maximum. If $\tiny a$ is positive, then it is a minimum; if $\tiny a$ is negative, then it is a maximum.

$\small \small f(x)=-3(x-2)^2+9$

In this example, $\small \small a$ is negative, so the vertex is a maximum.

$\small h = 2$ and $\small k=9$

$\small (h,k)=(2,9)$

Report an Error

Example Question #1 : Maximum And Minimum

Determine the maximum or minimum of y=6-9x^2+6x .

Possible Answers:

$\textup{Minimum at }x=-\frac{1}{3}$

$\textup{Maximum at }x=-3$

$\textup{Maximum at }x=-\frac{1}{3}$

$\textup{Minimum at }x=\frac{2}{3}$

$\textup{Maximum at }x=\frac{1}{3}$

Correct answer:

$\textup{Maximum at }x=\frac{1}{3}$

Explanation:

Rewrite the equation by the order of powers.

y=-9x^2+6x+6

This is a parabola in standard form: y=ax^2+bx+c

Determine the values of 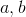a, b to the vertex formula.

$x=-\frac{b}{2a}=-\frac{6}{2(-9)}= \frac{6}{18}=\frac{1}{3}$

Since the leading coefficient of the parabola is negative, the parabola will curve downward and will have a maximum point.

Therefore there is a maximum at,

$x=\frac{1}{3}$ .

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Robert
Certified Tutor

Daytona State College, Bachelor in Arts, Teaching English as a Second Language (ESL).

View SAT Subject Test in Mathematics Level 1 Tutors

Patrick
Certified Tutor

LeTourneau University, Bachelors, Electrical Engineering. LeTourneau University, Masters, Electrical Engineering.

View SAT Subject Test in Mathematics Level 1 Tutors

Rima
Certified Tutor

Lebanese university , Master's/Graduate, Marketing and Management .

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Miami, SSAT Tutors in Philadelphia, Reading Tutors in Boston, SSAT Tutors in Miami, Physics Tutors in Dallas Fort Worth, English Tutors in Philadelphia, MCAT Tutors in Seattle, Calculus Tutors in Phoenix, LSAT Tutors in Chicago, Biology Tutors in Los Angeles

Popular Courses & Classes

LSAT Courses & Classes in Los Angeles, ACT Courses & Classes in San Diego, GRE Courses & Classes in Denver, LSAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Boston, LSAT Courses & Classes in Philadelphia, SSAT Courses & Classes in New York City, SAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Chicago, GRE Courses & Classes in Chicago

Popular Test Prep

SSAT Test Prep in Boston, GRE Test Prep in Atlanta, MCAT Test Prep in Washington DC, ACT Test Prep in San Diego, LSAT Test Prep in Washington DC, LSAT Test Prep in Philadelphia, ISEE Test Prep in Atlanta, MCAT Test Prep in Phoenix, ISEE Test Prep in Washington DC, GMAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Properties of Functions and Graphs

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #41 : Properties Of Functions And Graphs

Example Question #41 : Functions And Graphs

Example Question #1 : Maximum And Minimum

Example Question #1 : Maximum And Minimum

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: