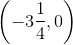Parallel lines never intersect, so you are looking for a line that has the same slope as the one given. The slope of the given line is –4, and the slope of the line in y = –4x + 5 is –4 as well. Since these two lines have equal slopes, they will run parallel and can never intersect.

First, put in slope-intercept form. 

. 

To find the -intercept, set  and solve for .

To find the y-intercept, set x equal to zero and solve for y.

This gives y = 3(0)² + 2(0) +7 = 7.

The equation for a line is:

, or in this case

We can solve for by plugging in the values given

Our line is now

Our x-intercept occurs when , so plugging in and solving for :

Volume of Cube = side³ = (4”)³ = 64 in³

Volume of Sphere = (4/3) * π * r³ = (4/3) * π * 1³ = (4/3) * π * 1³ = (4/3) * π = 4.187 in³

Difference = Volume of Cube – Volume of Sphere = 64 – 4.187 = 59.813 in³

The formula for the volume of a sphere is 4πr³/3. Because this formula is in terms of the radius, it would be easier for us to determine how the change in the radius affects the volume. Since we are told the diameter is doubled, we need to first determine how the change in the diameter affects the change in radius.

Let us call the sphere's original diameter d and its original radius r. We know that d = 2r.

Let's call the final diameter of the sphere D. Because the diameter is doubled, we know that D = 2d. We can substitute the value of d and obtain D = 2(2r) = 4r.

Let's call the final radius of the sphere R. We know that D = 2R, so we can now substituate this into the previous equation and write 2R = 4r. If we simplify this, we see that R = 2r. This means that the final radius is twice as large as the initial radius.

The initial volume of the sphere is 4πr³/3. The final volume of the sphere is 4πR³/3. Because R = 2r, we can substitute the value of R to obtain 4π(2r)³/3. When we simplify this, we get 4π(8r³)/3 = 32πr³/3.

In order to determine the factor by which the volume has increased, we need to find the ratio of the final volume to the initial volume.

32πr³/3 divided by 4πr³/3 = 8

The volume has increased by a factor of 8. 

Volume of a sphere is 4Πr³/3. Setting that equation equal to the original volume, the new volume is given as 8*4Πr³/3, which can be rewritten as 4Π8r³/3, and can be added to the radius value by 4Π(2r)³/3 since 8 si the cube of 2. This means the radius goes up by a factor of 2

Careful not to mix up radius and diameter. First, we need to identify that the second ball has a radius that is 4 times as large as the first ball.  The radius of the first ball is (1/2)x and the radius of the second ball is 2x. The volume of the second ball will be 4³, or 64 times bigger than the first ball.  So the second ball has a volume of 2 * 64 = 128.

The solution to this is simple, though just take it step-by-step.  First find the radius of the circular cross-section.  This will give us the radius of the sphere (since this cross-section is at the center of the sphere).  If the cross-section has an area of 225π, we know its area is defined by:

A = 225π = πr²

Solving for r, we get r = 15.

From here, we merely need to use our formula for the volume of a sphere:

V = (4 / 3)πr³

For our data this is: (4 / 3)π * 15³ = 4π * 15² * 5 = 4500π

We need to ascertain two values: The center point and the point of intersection with the surface.  Let's do that first:

The center is defined by the x-intercept. To find that, set the line equation equal to 0 (y = 0 at the x-intercept):

0 = 4x + 12; 4x = –12; x = –3; Therefore, the center is at (–3,0)

Next, we need to find the point at which the line intersects with the sphere's surface. To do this, solve for the point with x-coordinate at 3:

y = 4 * 3 + 12; y = 12 + 12; y = 24; therefore, the point of intersection is at (3,24)

Reviewing our data so far, this means that the radius of the sphere runs from the center, (–3,0), to the edge, (3,24).  If we find the distance between these two points, we can ascertain the length of the radius.  From that, we will be able to calculate the volume of the sphere.

The distance between these two points is defined by the distance formula:

d = √( (x₁ – x₀)² + (y₁ – y₀)² )

For our data, that is:

√( (3 + 3)² + (24 – 0)² ) = √( 6² + 24² )  = √(36 + 576) = √612 = √(2 * 2 * 3 * 3 * 17) = 6√(17)

Now, the volume of a sphere is defined by: V = (4/3)πr³

For our data, that would be:  (4/3)π * (6√(17))³ = (4/3) * 6³ * 17√(17) * π = 4 * 2 * 6² * 17√(17) * π = 4896π√(17)