All Precalculus Resources
Example Questions
Example Question #261 : Pre Calculus
Solve for all x on the interval
Solve for all x on the interval
Remember Soh, Cah, Toa?
For this problem it helps to recall that
Since our tangent is equal to 1 in this problem, we know that our opposite and adjacent sides must be the same (otherwise we wouldn't get "1" when we divided them)
Can you think of any angles in the first quadrant which yield equal x and y values?
If you guessed 


Example Question #262 : Pre Calculus

The above triangle is a right triangle. Find the value of 
One can setup the relationship

After taking the arccosine,
the arccosine cancels out the cosine leaving just the value of 
Example Question #3 : Find The Degree Measure Of An Angle For Which The Value Of A Trigonometric Function Is Known

What is the value of 
One can setup the relationship

After taking the arctangent,
the arctangent cancels out the tangent and we are left with the value of 
Example Question #4 : Find The Degree Measure Of An Angle For Which The Value Of A Trigonometric Function Is Known
Solve for 






If the sine of an angle, in this case 



Then we need to solve for theta by dividing by 3:
Example Question #5 : Find The Degree Measure Of An Angle For Which The Value Of A Trigonometric Function Is Known
Which of the following could be a value of 
Which of the following could be a value of 
To begin, it will be helpful to recall the following property of tangent:
This means that if 
The only place where we will have equal values for sine and cosine will be at the locations halfway between our quadrantal angles (axes). In other words, our answer will align with one of the angles.
Additionally, because our sine and cosine must have opposite signs (one negative and one positive), we need to be in either quadrant 2 or quadrant 4. There is only answer from either of those two, so our answer must be 
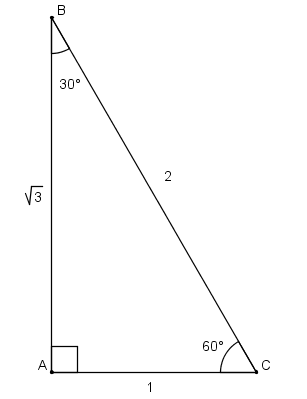
Example Question #6 : Find The Degree Measure Of An Angle For Which The Value Of A Trigonometric Function Is Known
Find 

Since we know the value of the trigonometric function and the triangle is located in Quadrant I, we can draw the triangle and get a sense of it. If the opposite side is 1 and the hypotenuse is 2, we know that we're dealing with a 30-60-90 special triangle. And since the opposite side of the angle is 1, we know that the angle is 
Example Question #7 : Find The Degree Measure Of An Angle For Which The Value Of A Trigonometric Function Is Known
Given the equation 

Find 1 possible value of 
Recall that
So if , then
Thinking back to our unit circle, recall that cosine corresponds to the x-value. Therefore, we must be in quadrants II or III.
So, which angles correspond to an x-value of -0.5? Well, they must be the angles closest to the y-axis, which are our 
This means our angle must be either
or
It must be 
Note that there are technically infinte solutions, because we are not given a specific interval. However, we only need to worry about one.
Example Question #1 : Circular Functions
What is the sine of an angle if a point on the terminal side of the angle is 
Given the point on the coordinate plane 
The hypotenuse of the right triangle formed by the origin and the point is 
The length of the triangle is 1 unit, and the height of the triangle is 5.
Sine of an angle is opposite side divided by the hypotenuse.
Rationalize the denominator.
Example Question #42 : Trigonometric Functions
Please choose the best answer from the following choices.
Find the secant value of 
First, use the Pythagorean Theorem to solve for all the sides of the triangle. You know that the adjacent side is 4 units long, and the opposite side is -9 units long.
Using the Pythagorean Theorem, you should get a hypotenuse of 
Secant is defined as hypotenuse/opposite.
Thus, giving you an answer of 
Example Question #1 : Find The Value Of The Sine Or Cosine Functions Of An Angle Given A Point On Its Terminal Side
Find the sine value of 
This is a 30-60-90 triangle. A 30-60-90 triangle will have leg lengths of 

All Precalculus Resources








































































