Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Trigonometric Applications

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #6 : Law Of Cosines And Sines

Lc1c

What is the measurement of side using the Law of Cosines? Round to the nearest tenth.

Possible Answers:

234.2m

234m

234.3m

235m

Correct answer:

234.3m

Explanation:

The Law of Cosines for side is,

$a^2=b^2+c^2-2bc\cdot cosA$ .

Plugging in the information we know, the formula is,

a^2=400^2+375^2-2(400)(375)cos(35)=54879.38671 .

Then take the square of both sides: a=234.2634985 .

Finally, round to the appropriate units: a=234.3m .

Report an Error

Example Question #11 : Law Of Cosines And Sines

Use the Law of Cosines to solve for the specified variable.

Pcq1

A=36.870

b=4

c=5

Solve for . Round to the nearest tenth.

Possible Answers:

None of these answers are correct.

$\frac{-32}{-40}$

Correct answer:

Explanation:

Law of Cosines

$a^2=b^2+c^2-2bc \cos A$

Therefore...

$a^2=16+25-2(4)(5)(\cos 36.9)$

$a^2=41-40(\cos 36.9)$

a^2=41-31.987

a^2=9.01

a=3.00

After rounding...

a=3

Report an Error

Example Question #51 : Trigonometric Applications

Use the Law of Sines to find in the following triangle.

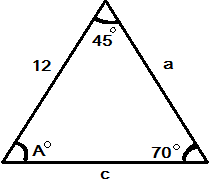
(Not drawn to scale.)

Possible Answers:

c=9.03

c=7.52

c=14.4

c=15.95

c=13.29

Correct answer:

c=9.03

Explanation:

We use the Law of Sines to solve this problem

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$

we plug in $b=12, B=70^{\circ}, C=45^{\circ}$

$\frac{12}{\sin 70^{\circ}}=\frac{c}{\sin 45^{\circ}}$

solving for we get:

$c=\frac{12\times \sin 45^{\circ}}{\sin 70^{\circ}}=9.03$

Report an Error

Example Question #52 : Trigonometric Applications

Use the Law of Sines to find .

(Not drawn to scale.)

Possible Answers:

b=2.9

b=6.52

b=7.17

b=23.56

b=14.29

Correct answer:

b=7.17

Explanation:

We use the Law of Sines to solve this problem:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$

where $A=65^{\circ}, B=30^{\circ}, C=85^{\circ}, a=13$

We plug in the values that we will need:

$\frac{13}{\sin 65^{\circ}}=\frac{b}{\sin 30^{\circ}}$

Notice that we did not use .

Solve for we get:

$b=\frac{13\times \sin 30^{\circ}}{\sin 65^{\circ}}=7.17$

Report an Error

Example Question #53 : Trigonometric Applications

Which of the following are the missing sides of the triangle?

$\text{I. } 13.95$

$\text{II. }6.55$

$\text{III. }4.59$

$\text{IV. }9.77$

Possible Answers:

$\text{II and III}$

None of the above

$\text{I and III}$

$\text{II and IV}$

Correct answer:

$\text{II and III}$

Explanation:

In order to solve this problem, we need to find . We do so by remembering the sum of the angles in a triangle is $180^{\circ}$ :

$C=180^{\circ}-55^{\circ}-35^{\circ}=90^{\circ}$

We can now use the Law of Sines to find the missing sides.

$\frac{a}{\sin 55}=\frac{8}{\sin 90}$

$a=\frac{8\times \sin 55}{\sin 90}=6.55$ which is II.

$\frac{b}{\sin 35}=\frac{8}{\sin 90}$

$b=\frac{8\times \sin 35}{\sin 90}=4.59$ which is III.

Our answers are then II and III

Report an Error

Example Question #15 : Law Of Cosines And Sines

Which of the following are the missing sides of the triangle?

$\text{I. }4.55$

$\text{II. }5.49$

$\text{III. }1.72$

$\text{IV. }14.56$

Possible Answers:

$\text{II and IV}$

None of the above

$\text{I and II}$

$\text{I and III}$

Correct answer:

$\text{I and III}$

Explanation:

In order to solve this problem, we need to find

Since all the angles of a triangle add to $180^{\circ}$ , we can easily find it:

$180^{\circ}-65^{\circ}-20^{\circ}=95^{\circ}$

We can now use the Law of Sines to find the missing sides:

$\frac{a}{\sin 65}=\frac{5}{\sin 95}$

$a=\frac{5\times \sin 65}{\sin 95}=4.55$ which is I.

$\frac{b}{\sin 20}=\frac{5}{\sin 95}$

$b=\frac{5\times \sin 20}{\sin 95}=1.72$ which is III.

Our answers are then I and III.

Report an Error

Example Question #16 : Law Of Cosines And Sines

Solve the triangle using the Law of Sines:

Law_of_sines__aas_

Possible Answers:

$a = 5.64, \measuredangle A = 30^{\circ}, b = 8.55$

None of the other answers

$a=6.01, \measuredangle A=31^\circ, b=12$

$a = 5.81, \measuredangle A = 20^{\circ}, b = 10.34$

$a = 4.37, \measuredangle A = 20^{\circ}, b = 9.78$

Correct answer:

$a = 4.37, \measuredangle A = 20^{\circ}, b = 9.78$

Explanation:

First we need to know what the Law of Sines is:

$\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}$

Looking at the triangle, we know c, C, and B. We can either solve for side b, using the law, or angle A using our knowledge that the interior angles of a triangle must add up to be 180.

$\frac{b}{sin50^{\circ}} = \frac{12}{sin110^{\circ}}$

$b = \frac{12\cdot sin{50^{\circ}}}{sin110^{\circ}} = 9.78$

$A = 180^{\circ} - 110^{\circ} - 50^{\circ} = 20^{\circ}$

Now all that's left is to find side a:

$\frac{a}{sin20^{\circ}} = \frac{12}{sin110^{\circ}}$

$a = \frac{12\cdot sin{20^{\circ}}}{sin110^{\circ}} = 4.37$

Report an Error

Example Question #17 : Law Of Cosines And Sines

Use the Law of Sines to solve for the specified variable.

Pcq2

A=60

B=70

a=6

Solve for . Round to the nearest tenth.

Possible Answers:

4.9

5.6

0.1

None of these answers are correct.

6.5

Correct answer:

6.5

Explanation:

Law of Sines

$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$

Therefore...

$\frac{\sin A}{a} = \frac{\sin B}{b}$

$\frac{\sin 60}{6}= \frac{\sin 70}{b}$

$\sin 60 = \frac{6 \cdot \sin 70}{b}$

$b=\frac{6 \cdot \sin 70}{\sin 60}$

b=6.526

After rounding...

b=6.5

Report an Error

Example Question #18 : Use The Laws Of Cosines And Sines

Pcq2

Solve for c using Law of Sines, given:

B=70

C=50

b=6.5

Round to the nearest tenth.

Possible Answers:

None of these answers are correct.

5.3

0.7

5.0

1.1

Correct answer:

5.3

Explanation:

Law of Sines

$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$

Therefore...

$\frac{\sin 70}{6.5}=\frac{\sin 50}{c}$

$\sin 70 = \frac{6.5 \cdot \sin 50}{c}$

$c= \frac{6.5 \cdot \sin 50}{\sin 70}$

c=5.320

After rounding...

c=5.3

Report an Error

Example Question #54 : Trigonometric Applications

Triangle_700

Given b=4ft, c=6ft, and $B=36^\circ$ , what is the measurement of to the nearest degree?

Possible Answers:

$83^\circ$

$82^\circ$

$82.2^\circ$

$82.15^\circ$

Correct answer:

$82^\circ$

Explanation:

Using the information we have, we can solve for $\angle C$ :

$\frac{sinB}{b}=\frac{sinC}{c}$ .

Plugging in what we know, we have:

$\frac{sin(36)}{4}=\frac{sinC}{6}$ .

Then, solve for sinC :

$6\cdot\frac{sin(36)}{4}=sinC$ .

Simplify, then solve for : 0.8816778784=sinC which means $sin^{-1}(.8816778784)=C$ .

Therefore, after rounding to the nearest degree, $C=62^\circ$ .

To solve for $\angle A$ , subtract $\angle B$ and $\angle C$ from $180^\circ$ : $180^\circ-36^\circ-62^\circ=82^\circ$ .

Therefore, $\angle A = 82^\circ$ .

Report an Error

View Pre-Calculus Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

View Pre-Calculus Tutors

Samarth
Certified Tutor

Maharaja Sayajirao University of Baroda, Bachelor of Engineering, Mechanical Engineering. Concordia University-Seward, Master...

View Pre-Calculus Tutors

Muhammad
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Mechanical Engineering.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Los Angeles, Physics Tutors in Phoenix, SAT Tutors in Phoenix, MCAT Tutors in Atlanta, Statistics Tutors in Los Angeles, Reading Tutors in Boston, Calculus Tutors in Atlanta, English Tutors in Boston, LSAT Tutors in New York City, Computer Science Tutors in San Diego

Popular Courses & Classes

GRE Courses & Classes in Atlanta, MCAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Miami, LSAT Courses & Classes in Chicago, GMAT Courses & Classes in Seattle, MCAT Courses & Classes in Los Angeles, SAT Courses & Classes in Miami, Spanish Courses & Classes in Los Angeles, SSAT Courses & Classes in Philadelphia, SSAT Courses & Classes in San Diego

Popular Test Prep

ISEE Test Prep in Denver, LSAT Test Prep in Seattle, LSAT Test Prep in Washington DC, GMAT Test Prep in San Diego, SSAT Test Prep in San Diego, MCAT Test Prep in New York City, MCAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Phoenix, LSAT Test Prep in Los Angeles, SSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Trigonometric Applications

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #6 : Law Of Cosines And Sines

Example Question #11 : Law Of Cosines And Sines

Example Question #51 : Trigonometric Applications

Example Question #52 : Trigonometric Applications

Example Question #53 : Trigonometric Applications

Example Question #15 : Law Of Cosines And Sines

Example Question #16 : Law Of Cosines And Sines

Example Question #17 : Law Of Cosines And Sines

Example Question #18 : Use The Laws Of Cosines And Sines

Example Question #54 : Trigonometric Applications

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: