All Precalculus Resources
Example Questions
Example Question #1 : Triangles
Let ABC be a right triangle with sides 






We are looking for 

So therefore, without figuring out 
Example Question #1832 : High School Math
Simplify the function below:
We need to use the following formulas:
a)
and
b)
We can simplify 
Example Question #11 : Relations And Functions
Simplify

Example Question #1 : Trigonometric Identities
Simplify

and

Example Question #1831 : High School Math
If 

1
We can write:
We can also write:
Now we can substitute the values of (sinx - cosx) and (sinx * cosx) in the obtained function:
Example Question #12 : Relations And Functions
Identifying a function.
Which of the following is a function.
The only relation listed that doesn't map more than one dependent variable value for some independent variable value is h(x). Another way of saying this is that each value in the domain of h corresponds to a distinct value in its range. h(x) is the only one-to-one relation, and so is the only option that is a function.
Example Question #16 : Functions
Evaluating a function.
Evaluate 

Plug in -3 for x in the function rule:

Example Question #43 : Pre Calculus
Finding inverse functions.
Given,
find

To find an inversefunction find the input in terms of the output. In other words, solve the function for the dependent variable.
First, set h(x) = y. Now solve for y.
Multiply the denominator on both sides
Distribute y
Rearrange to get only x terms on one side.
Factor out x on the left side.
Divide by (y-5) on both sides to get x by itself.
The final step is to recognize that the independent variable is now the dependent variable. To put this into proper notation switch x and y. The inverse function is

Example Question #18 : Functions
Finding an inverse function.
Given
find



Finding an inverse function is essentially finding the output in terms of the input. To do this switch the independent and dependent variables. First set

Then
Now, to switch the role of the variables solve for x in terms of y.
or
So, y is now the independent variable, and x is the dependent variable. The final step is to write the inverse function in proper notation.
Set 

This gives

Example Question #13 : Relations And Functions
Which function below correctly translates 
The translation 







A vertical translation is up if 

Combining these, we get 
Certified Tutor
All Precalculus Resources








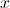





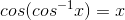







![[\cos(x)/\sin(x)]\times\sin(x)=\cos(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/27160/gif.latex)
























































