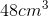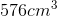We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Volume of a Pyramid

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Volume

Principal O'Shaughnessy has a paperweight in the shape of a pyramid with a square base. If one side of the base has a length of 4cm and the height of the paperweight is 6cm, what is the volume of the paperweight?

Possible Answers:

48cm^3

96cm^3

32cm^3

192cm^3

576cm^3

Correct answer:

32cm^3

Explanation:

We begin by recalling the volume of a pyramid.

$V=\frac{1}{3}Ah$

where is the area of the base and is the height.

Since the base is a square, we can find the area by squaring the length of one of the sides.

A=4^2=16

Given the height is 6cm, we can now calculate the volume.

$V=\frac{1}{3}(16)(6)=32$

Since all of the measurements were in centimeters, our volume will be in cubic centimeters.

Therefore, the volume of Principal O'Shaughnessy's paperweight is 32cm^3 .

Report an Error

Example Question #1 : Volume

The volume of a square pyramid is $162 m^{3}$ . If a side of the square base measures . What is the height of the pyramid?

Possible Answers:

4.5m

7.5m

Correct answer:

Explanation:

The formula for the volume of a pyramid is $\frac{\left ( B \times h\right )}{3}$ , where is the area of the base and is the height.

Using this formula,

= Area of the base, which is nothing but area of square with side . $9m \times 9m = 81 m^{2}$

Now, $\frac{81m^{2} \times h}{3} = 162 m^{3}$ when simplified, you get .

Hence, the height of the pyramid is .

Report an Error

Example Question #1 : How To Find The Volume Of A Pyramid

A pyramid has height 4 feet. Its base is a square with sidelength 3 feet. Give its volume in cubic inches.

Possible Answers:

$124,416\textrm{ in}^{3}$

$31,104\textrm{ in}^{3}$

$62,208 \textrm{ in}^{3}$

$20,736 \textrm{ in}^{3}$

$5,184\textrm{ in}^{3}$

Correct answer:

$20,736 \textrm{ in}^{3}$

Explanation:

Convert each measurement from inches to feet by multiplying it by 12:

Height: 4 feet = $4 \times 12 = 48$ inches

Sidelength of the base: 3 feet = $3 \times 12 = 36$ inches

The volume of a pyramid is

$V = \frac{1}{3} Bh$

Since the base is a square, we can replace $B = s^{2}$ :

$V = \frac{1}{3} s ^{2}h$

Substitute s=36, h = 48

$V = \frac{1}{3} \cdot 36 ^{2}\cdot 48$

V =20,736

The pyramid has volume 20,736 cubic inches.

Report an Error

Example Question #3 : Volume

The height of a right pyramid is feet. Its base is a square with sidelength feet. Give its volume in cubic inches.

Possible Answers:

$62,208\textrm{ in}^{3}$

$10,368 \textrm{ in}^{3}$

$31,104 \textrm{ in}^{3}$

$15,552 \textrm{ in}^{3}$

$41,472 \textrm{ in}^{3}$

Correct answer:

$10,368 \textrm{ in}^{3}$

Explanation:

Convert each of the measurements from feet to inches by multiplying by .

Height: $2 \times 12 = 24$ inches

Sidelength of base: $3 \times 12 = 36$ inches

The base of the pyramid has area

$B = s^{2} = 36^{2} = 1,296$ square inches.

Substitute B = 1,296, h = 24 into the volume formula:

$V = \frac {1}{3} Bh$

$V = \frac {1}{3} \cdot 1,296 \cdot 24 =10,368$ cubic inches

Report an Error

Example Question #322 : Isee Upper Level (Grades 9 12) Mathematics Achievement

The height of a right pyramid and the sidelength of its square base are equal. The perimeter of the base is 3 feet. Give its volume in cubic inches.

Possible Answers:

$27 \textrm{ in}^{3}$

$81 \textrm{ in}^{3}$

$576 \textrm{ in}^{3}$

$243 \textrm{ in}^{3}$

$729 \textrm{ in}^{3}$

Correct answer:

$243 \textrm{ in}^{3}$

Explanation:

The perimeter of the square base, feet, is equivalent to $3 \times 12 = 36$ inches; divide by to get the sidelength of the base - and the height: $36 \div 4 = 9$ inches.

The area of the base is therefore $B = s^{2} = 9^{2} = 81$ square inches.

In the formula for the volume of a pyramid, substitute B = 81,h=9 :

$V = \frac{1}{3} Bh = \frac{1}{3}\cdot 81 \cdot 9 = 243$ cubic inches.

Report an Error

Example Question #1 : How To Find The Volume Of A Pyramid

What is the volume of a pyramid with the following measurements?

$length=7; width=6;height=9;slant\ length=11$

Possible Answers:

462

378

154

126

Correct answer:

126

Explanation:

The volume of a pyramid can be determined using the following equation:

$V=\frac{1}{3}lwh=\frac{1}{3}(7)(6)(9)=126$

Report an Error

Example Question #1 : Volume Of A Pyramid

The pyramid has a length, width, and height of 2,4,6 respectively. What is the volume of the pyramid?

Possible Answers:

Correct answer:

Explanation:

Write the formula for the volume of a pyramid.

$V=\frac{1}{3} (L\times W\times H)$

Substitute the dimensions and solve.

$V=\frac{1}{3} (2\times 4\times 6) = \frac{1}{3}(48)=16$

Report an Error

Example Question #2 : Volume

If the base area of the pyramid is , and the height is , what is the volume of the pyramid?

Possible Answers:

Correct answer:

Explanation:

Write the volume formula for the pyramid.

$V=\frac{1}{3} (L\times W\times H)$

The base area is represented by $L\times W$ .

Substitute the knowns into the formula.

$V=\frac{1}{3} (2\times 3) = \frac{1}{3} (6) =2$

Report an Error

Example Question #2 : Volume

Find the volume of a pyramid with a length of 4, width of 7, and a height of 3.

Possible Answers:

Correct answer:

Explanation:

Write the formula to find the area of a pyramid.

$V=\frac{1}{3} (L\times W \times H)$

Substitute the dimensions.

$V=\frac{1}{3} (4\times 7\times 3) = 28$

Report an Error

Example Question #4 : Volume

Find the volume of a pyramid if the length, base, and height are $\textup{10, 20, and 40,}$ respectively.

Possible Answers:

400

500

$\frac{400}{3}$

$\frac{800}{3}$

$\frac{8000}{3}$

Correct answer:

$\frac{8000}{3}$

Explanation:

Write the formula for the volume of a pyramid.

$V=\frac{1}{3} (LWH)$

Substitute the dimensions and solve for the volume.

$V=\frac{1}{3} (10)(20)(40) = \frac{8000}{3}$

Report an Error

View Pre-Algebra Tutors

Timothy
Certified Tutor

Bethune-Cookman University, Bachelor of Science, Mathematics. University of Phoenix, Master of Science, Computer and Informat...

View Pre-Algebra Tutors

Shifrah
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Biology, General. Massachusetts College of Pharmacy and Health ...

View Pre-Algebra Tutors

Donald
Certified Tutor

Bowling Green State University-Main Campus, Bachelor of Science, Geology. Bowling Green State University-Main Campus, Master ...

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Denver, ISEE Tutors in Miami, Statistics Tutors in Philadelphia, MCAT Tutors in Denver, ACT Tutors in Denver, Statistics Tutors in Miami, Calculus Tutors in Seattle, ACT Tutors in Houston, Spanish Tutors in Boston, Chemistry Tutors in Houston

Popular Courses & Classes

ISEE Courses & Classes in New York City, Spanish Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Boston, ACT Courses & Classes in Washington DC, LSAT Courses & Classes in Houston, MCAT Courses & Classes in Phoenix, GRE Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in San Diego, GRE Courses & Classes in Miami

Popular Test Prep

ACT Test Prep in Washington DC, ISEE Test Prep in Atlanta, LSAT Test Prep in Seattle, ISEE Test Prep in New York City, ISEE Test Prep in Los Angeles, ACT Test Prep in Los Angeles, GMAT Test Prep in Washington DC, ACT Test Prep in Boston, SSAT Test Prep in Miami, GRE Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Volume of a Pyramid

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #1 : Volume

Example Question #1 : Volume

Example Question #1 : How To Find The Volume Of A Pyramid

Example Question #3 : Volume

Example Question #322 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #1 : How To Find The Volume Of A Pyramid

Example Question #1 : Volume Of A Pyramid

Example Question #2 : Volume

Example Question #2 : Volume

Example Question #4 : Volume

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: