All Pre-Algebra Resources
Example Questions
Example Question #1 : Volume Of A Cone
Find the volume of a cone with a radius of 

Write the volume formula for a cone.
Substitute the dimensions.
Example Question #7 : Volume Of A Cone
Find the volume of the cone that has a radius of 

Write the formula to find the volume of a cone.
Example Question #8 : Volume Of A Cone
Find the volume of a cone with a radius of 

Write the formula to find the volume of the vone.
Substitute the dimensions into the formula.
Expand the terms.
Multiply the integers for the volume.
Example Question #211 : Geometry
Solve for the volume of a cone with a circular area of 

Write the formula for the volume of a cone.
The area of the circular base is represented as 
Substitute 
Multiply out each term and leave 
Example Question #11 : Volume Of A Cone
You have an ice cream cone. You want to fill the cone completely with ice cream. What is the volume of ice cream you can fill it with if the height of the cone is 12cm and the diameter is 8cm?
The formula to find the volume of a cone is
where r is the radius and h is the height. We know the diameter of the ice cream cone is 8cm. We also know the radius is half the diameter, so the radius is 4cm. We know the height is 12cm. Using substitution, we get
Example Question #211 : Geometry
A certain children's basketball has a diameter of 6 inches. What is the volume of the basketball?
Math involves a lot of formulas. Unfortunately that means we either have to do some memorization or compile a really long list of formulas for reference. Either way, a basketball is a sphere, which means we have to know the formula for the volume of a sphere to solve this problem.


Since our original unit was inches, and volume is always expressed in cubic units, our final answer is
Example Question #503 : Grade 8
In terms of 
20 feet = 



Example Question #504 : Grade 8
A sphere has diameter 3 meters. Give its volume in cubic centimeters (leave in terms of 
The diameter of 3 meters is equal to 


Example Question #1 : Volume Of A Three Dimensional Figure
A car dealership wants to fill a large spherical advertising ballon with helium. It can afford to buy 1,000 cubic yards of helium to fill this balloon. What is the greatest possible diameter of that balloon (nearest tenth of a yard)?
The volume of a sphere, given its radius, is
Set 

The diameter is twice this, or 12.4 yards.
Example Question #212 : Geometry
The diameter of a sphere is 
The formula for finding volume of a sphere is:

We are given the diameter, so to find radius we divide the diameter by 
We plug this radius into the formula:
All Pre-Algebra Resources











































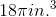































![r \approx \sqrt[3]{238.7} \approx 6.2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/92097/gif.latex)












