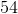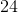We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Area

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #71 : Area

Find the area of the parallelogram if the base side is and the height is .

Possible Answers:

30x^2

15x^2

$\frac{15}{2}x^2$

16x

Correct answer:

15x^2

Explanation:

Write the area of the parallelogram.

A=bh

Substitute the dimensions.

A=(3x)(5x) = 15x^2

Report an Error

Example Question #72 : Area

Find the area of a parallelogram if the base is 13 and the height is 9.

Possible Answers:

112

117

224

Correct answer:

117

Explanation:

Write the formula for the area of a parallelogram.

A=bh

Substitute the base and height into the equation.

A=(13)(9) = 117

When multiplying two integers first multiply the ones place from each integer:

$9\cdot 3=27$

The seven will stay in the ones place but the two will be carried over. Now multiply the one integer with the tens integer and add the carried over term to that:

(9) (1)+2=9+2=11

The eleven represents the hundreds and tens spot. To get the final answer combine the ones digit to the hundreds and tens digit:

110+7=117

Report an Error

Example Question #73 : Area

Find the area of a parallelogram with the base of 5x^3 and a height of 10x^2 .

Possible Answers:

30 x^6

15 x^5

50 x^6

50 x^5

15 x^6

Correct answer:

50 x^5

Explanation:

Write the area formula of a parallelogram.

A=bh

Substitute the dimensions.

A=(5x^3)(10x^2)

Separate out the terms for clarity.

$A=5\cdot x\cdot x\cdot x\cdot 10\cdot x \cdot x$

There are five which could be combined as x^5 . Multiply the integers as well.

The area is: 50 x^5

Report an Error

Example Question #24 : Area Of A Parallelogram

Solve for the area of a parallelogram if the base is and the height is .

Possible Answers:

102

408

204

297

594

Correct answer:

297

Explanation:

Write the formula for the area of a parallelogram.

$A=\textup{ Base} \times \textup{ Height}$

Substitute the base and the height into the equation.

A=3(99) = 297

The area of the parallelogram is 297 .

Report an Error

Example Question #74 : Area

If the parallelogram base is 5 inches and the height is 8 inches, what must be the area of the parallelogram in inches?

Possible Answers:

$40 \textup{ inches}^2$

$20 \textup{ inches}^2$

$\frac{10}{3} \textup{ inches}^2$

$40 \textup{ inches}$

$\frac{10}{3} \textup{ inches}$

Correct answer:

$40 \textup{ inches}^2$

Explanation:

Write the area formula for a parallelogram.

$A=\textup{Base} \times \textup{Height}$

Substitute the dimensions into the formula.

$A= 5 \textup{ inches} \times 8 \textup{ inches} = 40 \textup{ inches}^2$

The area is always in units squared.

Report an Error

Example Question #27 : Area Of A Parallelogram

Find the area of a parallelogram with a base edge of and a height of .

Possible Answers:

31.5

Correct answer:

Explanation:

Write the formula for the area of a parallelogram.

A=bh

Substitute the base and the height into the formula and multiply the dimensions.

A=(9)(7) = 63

Report an Error

Example Question #75 : Area

Find the area of a parallelogram with a base of 9cm and height that is half the base.

Possible Answers:

$40.5\text{cm}^2$

$40.5\text{cm}$

$36\text{cm}$

$36.5\text{cm}^2$

$81\text{cm}^2$

Correct answer:

$40.5\text{cm}^2$

Explanation:

The formula to find the area of a parallelogram is

$A=b \cdot h$

where b is the base and h is the height. We know the base is 9cm and the height is half of the base. Therefore, the height is 4.5cm. Substituting into the formula, we get

$A = 9\text{cm} \cdot 4.5\text{cm}$

$A = 40.5\text{cm}^2$

Report an Error

Example Question #71 : Area

Find the area of the triangle:
Problem_12

Possible Answers:

Correct answer:

Explanation:

The area of the triangle can be determined using the following equation:
$\small A=\frac{1}{2}bh$

The base is the side of the triangle that is intersected by the height.

$\small A=\frac{1}{2}(4)(12)=(2)(12)=24$

Report an Error

Example Question #2 : Area Of A Triangle

The length of the base of a triangle is inches. The height of the triangle is inches. Find the area of the triangle.

Possible Answers:

$7.5\:in^{2}$

$50\:in^{2 }$

$15\:in^{2}$

$30\:in^{2}$

$25\:in^{2}$

Correct answer:

$25\:in^{2}$

Explanation:

The correct answer is $Area = 25 in^{2}$ .

The formula for the area of a triangle is $\frac{1}{2}\times base\times height$ .

To solve the equation, plug in the base and height: $\frac{1}{2} \cdot5\cdot10$

Once you multiply these three numbers, the answer you find is .

The units for area are always squared, so the unit is $in^{2}$ .

Report an Error

Example Question #3 : Area Of A Triangle

If a right triangle has dimensions of inches by inches by inches, what is the area?

Possible Answers:

$12\textup{ in} ^2$

$6\textup{ in} ^2$

$8\textup{ in} ^2$

$4\textup{ in} ^2$

Correct answer:

$6\textup{ in} ^2$

Explanation:

The question is asking you to find the area of a right triangle.

First you must know the equation to find the area of a triangle,

$A=\frac{1}{2}( base \cdot height)$ .

A right triangle is special because the height and base are always the two smallest dimensions.

This makes the equation

$\frac{1}{2}( 3\cdot 4)=\frac{1}{2}\cdot 12=\frac{12}{2}=6$

Report an Error

View Pre-Algebra Tutors

Michelle
Certified Tutor

University of Nevada-Las Vegas, Bachelor of Science, Mathematics.

View Pre-Algebra Tutors

Dejuan
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Electrical Engineering.

View Pre-Algebra Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Denver, MCAT Tutors in Boston, Computer Science Tutors in Washington DC, Biology Tutors in Boston, LSAT Tutors in Los Angeles, Calculus Tutors in Atlanta, Chemistry Tutors in San Diego, Math Tutors in Denver, Physics Tutors in New York City, French Tutors in Chicago

Popular Courses & Classes

GRE Courses & Classes in Denver, GRE Courses & Classes in Miami, ISEE Courses & Classes in Chicago, LSAT Courses & Classes in New York City, GRE Courses & Classes in New York City, GMAT Courses & Classes in Chicago, GMAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Chicago, ACT Courses & Classes in Chicago, GRE Courses & Classes in Boston

Popular Test Prep

GMAT Test Prep in Chicago, SSAT Test Prep in Philadelphia, ISEE Test Prep in Chicago, LSAT Test Prep in Boston, SAT Test Prep in Dallas Fort Worth, LSAT Test Prep in New York City, ACT Test Prep in Chicago, ACT Test Prep in Houston, SAT Test Prep in Denver, GMAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Area

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #71 : Area

Example Question #72 : Area

Example Question #73 : Area

Example Question #24 : Area Of A Parallelogram

Example Question #74 : Area

Example Question #27 : Area Of A Parallelogram

Example Question #75 : Area

Example Question #71 : Area

Example Question #2 : Area Of A Triangle

Example Question #3 : Area Of A Triangle

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: