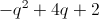All New SAT Math - No Calculator Resources
Example Questions
Example Question #201 : New Sat
For 

The complex conjugate of a complex number 



Example Question #1102 : Algebra
Set up the equation:
The difference of six and a number squared is four.
Write the following sentence by parts.
A number squared:
The difference of six and a number squared:
Is four:
Combine the parts to write an equation.
The answer is:
Example Question #202 : New Sat
Billy buys a tomato plant that is 4 inches tall. With regular watering the plant grows 3 inches a year. Writing Billy's plant's height as a function of time, what does the 
There is no 
The 
The 
The 
The 
The 
To solve this problem, first recall the equation of a line.
where
Remember that slope is the rate of change that occurs in a function and that the 


Now, identify what is known.
"Billy buys a tomato plant that is 4 inches tall. With regular watering the plant grows 3 inches a year."
Since the height of Billy's plant is 4 inches tall when he gets it, at time being zero. It is also stated that the plant grows 3 inches per year, this is the rate of change of the plant's height. Writing the known information in mathematical terms results as follows.
In this case our
Therefore, the 
Example Question #201 : New Sat
Billy buys a tomato plant that is 4 inches tall. With regular watering the plant grows 3 inches a year. Writing Billy's plant's height as a function of time, what does the slope represent?
The slope represents the rate of change in the height of the plant which is 3 inches per year.
The slope represents the starting height of the plant which is 3 inches.
The slope is zero.
The slope represents the rate of change in the height of the plant which is 4 inches per year.
The slope represents the starting height of the plant which is 4 inches.
The slope represents the rate of change in the height of the plant which is 3 inches per year.
To solve this problem, first recall the equation of a line.
where
Remember that slope is the rate of change that occurs in a function and that the 


Now, identify what is known.
"Billy buys a tomato plant that is 4 inches tall. With regular watering the plant grows 3 inches a year."
Since the height of Billy's plant is 4 inches tall when he gets it, at time being zero. It is also stated that the plant grows 3 inches per year, this is the rate of change of the plant's height. Writing the known information in mathematical terms results as follows.
In this case our
Therefore, the slope represents the rate of change in the height of the plant which is 3 inches per year.
Example Question #202 : New Sat
Simplify the following expression:
This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.
Add like terms together:

Combine these terms into one expression to find the answer:
Example Question #202 : New Sat
Solve for 
To solve for 
Now, simplify the first fraction by calculating four squared.
From here, factor the denominator of the second fraction.
Next, factor the 16.
From here, cancel out like terms that are in both the numerator and denominator. In this particular case that includes (x-2) and 2.
Now, distribute the eight.
Next, multiply both sides by the denominator.
The (8x+16) cancels out and leaves the following equation.
Now to solve for 

Example Question #203 : New Sat
Use substitution to solve to calculate 

To solve this problem first manipulate the given equation to solve for 
Multiply by 

Now to calculate 

Example Question #204 : New Sat
Find the solution 
We can solve either by substitution or by elimination. We will solve by elimination.
Line up both equations so the variables are in the same order.
Because we have a negative 


Solve for 
Plug 





The final answer will be 
Example Question #205 : New Sat
Calculate 

This question is testing the knowledge and skills of calculating a function value. Similar to domain and range, calculating the function value requires the application of input values into the function to find the output value. In other words, evaluating a function at a particular value results in the function value; which is another way of saying function value is the output.
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the input value.
Since the function is in the form 

Step 2: Given the function, input the desired 
In step one the input value of six was found. Now substitute 6 in for every
Step 3: Verify solution by graphing the function.

To find the function value on a graph go to 



Recall that 
Example Question #206 : New Sat
Sally spent $5.75 on pens and pencils for school. Each pencil cost 25 cents, and each pen cost 50 cents. If the number of pens Sally bought is one more than the number of pencils she bought, how many pencils and pens did she buy altogether?
Let x be the number of pencils and y be the number of pens Sally purchased. We are told that each pencil costs 25 cents. Because, the total amount she spent was given in dollars, we want to convert 25 cents to dollars. Because there are 100 cents in one dollar, 25 cents = $0.25. Similarly, each pen costs $0.50.
The amount that Sally spent on pencils is equal to the product of the number of pencils and the cost per pencil. We can model the amount of money spent on pencils as 0.25x.
Likewise, the amount Sally spent on pens is equal to the product of the number of pens and the cost per pen, or 0.5y.
Since we are told that Sally spent $5.75 total on pens and pencils combined, we can write the following:
We are also told that the number of pens is one greater than the number of pencils. We can thus write:
We now have two equations and two unknowns. In order to solve this system of equations, we can take the value of y = x + 1 and substitute it into the other equation.
Distribute.
Combine x terms.
Subtract 0.5 from both sides.
Divide both sides by 0.75.
This means Sally bought 7 pencils and 8 pens. The question asks us to find the number of pens and pencils purchased altogether, which would equal
The answer is 15.
Certified Tutor
Certified Tutor
All New SAT Math - No Calculator Resources