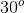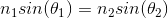Call Now to Set Up Tutoring:

(888) 888-0446

MCAT Physical : General Principles and Properties

Study concepts, example questions & explanations for MCAT Physical

Create An Account

All MCAT Physical Resources

8 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #121 : Ap Physics 2

A monochromatic light ray passes from air (n = 1.00) into glass (n = 1.50) at an angle of 20^o with respect to the normal. What is the approximate angle of refraction?

Possible Answers:

17^o

13^o

24^o

27^o

31^o

Correct answer:

13^o

Explanation:

To compare angles of incidence and refraction, use Snell's law.

$n_{1}sin(\theta _{1})=n_{2}sin(\theta _{2})$

$1.00sin(20)=1.50sin(\theta _{2})$

$.228=sin(\theta _{2})$

$\theta _{2}=sin^{-1}(.228)=13.2^o$

Notice that as the light enters a more dense medium, it bends towards the normal.

Report an Error

Example Question #2 : Snell's Law

An incandescent light bulb is shown through a glass prism. The certain wavlength of the light is then directed into a glass cuvette containing an unknown concentration of protein. Commonly, this process is called spectroscopy and is used to determine the concentrations of DNA, RNA, and proteins in solutions. The indices of reflection of air, glass, and the solution are 1, 1.5, and 1.3, respectively.

The red light, selected for by the prism, is shown through air onto the glass cuvette at an angle of 30^o to the normal. At what angle to normal does the light have when it is in the glass?

Possible Answers:

30^o

45^o

19.5^o

22^o

Correct answer:

19.5^o

Explanation:

This problem asks us to consider refraction, that is, the bending of light when it enters a new medium. Thinking back to our light formulas in physics, we know that $n_1*\sin\theta_1 = n_2*\sin\theta_2$ , where n is the index of refraction of the medium and $\theta$ is the angle the light ray makes to normal.

Using the information provided in the pre-question text and the question above, we can solve for $\theta_2$ .

$n_1*\sin\theta_1 = n_2*\sin\theta_2$

$sin\theta_2 = \frac{n_1*\sin\theta_1}{n_2}$

$\theta_2 = \sin^{-1}(\frac{n_1*\sin\theta_1}{n_2}) = \sin^{-1}(\frac{1*sin (30^o)}{1.5}) = 19.5^{\circ}$

Report an Error

Example Question #3 : Snell's Law

Red light is selected for by the prism and shown onto the glass cuvette at an angle of 30^o to the normal. At what angle to normal does the light travel when it is in the solution after it has moved through wall of the cuvette?

Possible Answers:

22.7^o

35^o

45^o

19.5^o

Correct answer:

22.7^o

Explanation:

Notice that, in this problem, there are two different changes in indices of refraction: air to glass and glass to solution; thus, we need to compute the angle change twice. First, let’s look at how the angle changes from air to glass. We know from Snell’s law that $n_1*\sin\theta_1 = n_2*\sin\theta_2$ , where n is the index of refraction of the medium and $\theta$ is the angle the light ray makes to normal.

Rearranging, we can find the angle to normal in the glass.

$sin\theta_2 = \frac{n_1*\sin\theta_1}{n_2}$

$\theta_2 = \sin^{-1}(\frac{n_1*\sin\theta_1}{n_2}) = \sin^{-1}(\frac{1*sin (30^o)}{1.5}) = 19.5^{\circ}$

Now, we can use this angle and repeat the above equation to find the angle that the light enters the solution.

$n_2*\sin\theta_2 = n_3*\sin\theta_3$

$sin\theta_3 = \frac{n_2*\sin\theta_2}{n_3}$

$\theta_3 = \sin^{-1}(\frac{n_2*\sin\theta_2}{n_3}) = \sin^{-1}(\frac{1.5*sin (19.5^o)}{1.3}) = 22.7^{\circ}$

Report an Error

Example Question #21 : Optics

If the solution had a higher protein concentration than expected, how would the angle of refraction change as light travels from the glass into the solution?

Possible Answers:

It would be larger

It would be larger or smaller, depending on the color of the light

It would remain the same

It would be smaller

Correct answer:

It would be smaller

Explanation:

This question is asking us to consider what would happen if the solution were more concentrated, essentially, if there were more particles per unit volume (denser). If we think back to the definition of index of refraction, we know that it relates to the density of a medium. The denser the medium, the higher the index of refraction.

$n=\frac{c}{v}$

Looking at Snell’s law, we can see the relationship between index of refraction and the angle of refraction.

$n_1*\sin\theta_1 = n_2*\sin\theta_2$

$sin\theta_2 = \frac{n_1*\sin\theta_1}{n_2}$

If the solution were more concentrated, n₂ would increase, making the term on the right side of the equation smaller. The sin function of a smaller number gives a smaller angle; thus, as the concentration increases (and thus the index of refraction increases), the angle of refraction gets smaller.

Report an Error

Example Question #1 : Snell's Law

At what angle would the light passing through the glass cuvette need to hit the solution inside the cuvette for no light to enter the solution?

Possible Answers:

30^o

45^o

60^o

90^o

55^o

Correct answer:

60^o

Explanation:

First, we need to determine what this question is asking us to do. If no light entered the solution from the glass, we know this is total internal reflection. Remember that total internal reflection occurs when light from one medium hits a second medium at an angle higher that the critical angle. Thinking back to our physics formulas, we know that the critical angle can be determined by the equation below.

$\theta_c = \sin^{-1}(\frac{n_2}{n_1})$

Plugging in the values for glass and the solution, we can find the critical angle.

$\theta_c = \sin^{-1}(\frac{n_2}{n_1}) = \sin^{-1}(\frac{1.3}{1.5}) = \sin^{-1}(0.87)=60.1^{\circ}$

Report an Error

Example Question #1 : Total Internal Reflection

A scuba diver wearing a head lamp is returning to the surface of the Pacific Ocean. What is the index of refraction of the ocean water if the smallest angle resulting in total internal reflection is 35 degrees from the vertical?

$n_{air}=1.00$

Possible Answers:

1.22

1.74

0.82

1.98

0.57

Correct answer:

1.74

Explanation:

We can use Snell's law to calculate the index of refraction of the water:

$n_1sin(\theta_1) = n_2sin(\theta_2)$

Where the subscript 1 denotes water and subscript 2 denotes air.

At the first incidence of total internal reflection, the angle of refraction is 90 degrees. Therefore, the sine function becomes 1, giving us the formula:

$n_1sin(\theta_1) = n_2$

Rearranging for the index of water:

$n_1 = \frac{n_2}{sin(\theta_1)} = \frac{1}{sin(35)} = 1.74$

Report an Error

View MCAT Chemical and Physical Foundations of Biological Systems Tutors

Shrikar
Certified Tutor

University of South Florida-Main Campus, Bachelor of Science, Biomedical Sciences.

View MCAT Chemical and Physical Foundations of Biological Systems Tutors

Frank
Certified Tutor

Metropolitan State University of Denver, Bachelor of Science, Biochemistry. Kirksville College of Osteopathic Medicine, Non D...

View MCAT Chemical and Physical Foundations of Biological Systems Tutors

Christy
Certified Tutor

Northern Michigan University, Bachelor in Arts, Graphic Design. Northern Michigan University, Bachelor of Science, Premedicine.

All MCAT Physical Resources

8 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Phoenix, GMAT Tutors in Philadelphia, Reading Tutors in San Francisco-Bay Area, English Tutors in San Diego, Computer Science Tutors in Miami, GMAT Tutors in Washington DC, English Tutors in Chicago, Reading Tutors in Denver, Biology Tutors in Chicago, Spanish Tutors in San Francisco-Bay Area

Popular Courses & Classes

MCAT Courses & Classes in San Diego, ISEE Courses & Classes in Seattle, Spanish Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Denver, Spanish Courses & Classes in Washington DC, SSAT Courses & Classes in Los Angeles, LSAT Courses & Classes in New York City, GRE Courses & Classes in Miami, MCAT Courses & Classes in Chicago, LSAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

LSAT Test Prep in New York City, GMAT Test Prep in Denver, MCAT Test Prep in San Diego, ISEE Test Prep in Philadelphia, SAT Test Prep in Seattle, SSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in San Diego, GRE Test Prep in Washington DC, SSAT Test Prep in Washington DC, GMAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

MCAT Physical : General Principles and Properties

Study concepts, example questions & explanations for MCAT Physical

All MCAT Physical Resources

Example Questions

Example Question #121 : Ap Physics 2

Example Question #2 : Snell's Law

Example Question #3 : Snell's Law

Example Question #21 : Optics

Example Question #1 : Snell's Law

Example Question #1 : Total Internal Reflection

All MCAT Physical Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: