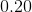The maximum force that the spring will exert on the mass is at maximum displacement from the equilibrium position. This can be seen with the formula for spring force.

 is the displacement and  is the spring constant. The reason that the right side of the formula is negative is because the force due to the spring is in the opposite direction of the displacement. The spring constant remains the same throughout the motion of the mass, therefore the maximum force will be generated when  (displacement) is greatest.

The equation best suited to solve this question is , where is the frequency of the motion, is the spring constant, and is the mass.

Two approaches can be used to solve for the period.

Since  , we can first solve for the frequency, and then solve for .  The second method is to rearrange the equation to directly solve for : . Either method can be used; it is simply a matter of preference.

Using the first method, we can plug in the given values from the question.

Now, we need to take the reciprocal of the frequency in order to solve for the period.

Since the period is the inverse of the frequency, the answer is .

Looking at the equation, we can see that the distance the spring is stretched or compressed has no effect on the period or frequency.

Hooke's law is written as , where k is the spring constant, and  is the change in position of the spring.

Since this is the upward force that will cancel out the downward force of the plant on the spring, we can set the forces equal to each other.

Hooke's law states the formula for the force of a spring:

The distorting force on a spring, whether lengthening or shortening, is opposed by the spring, hence the negative sign. In our question, the distorting force is caused by gravity acting on the mass, allowing us to set the force of the spring equal and opposite to the force fo gravity on the mass.

Use our given values for the spring constant, mass, and acceleration of gravity to find the resultant displacement.

Hanging the mass from the spring will cause it to stretch approximately .

There are a few steps to this problem. First we need to know the tension on the spring. From there we can calculate the spring constant, knowing the potential energy it is storing.

Let's draw in all of the forces to help visualize the system:

If the system is at equilibrum, then all of the forces must cancel out. Separating the forces into their components we get:

x-components:

y-components:

We can solve these equations simultaneously for T1 and T2. Since we only need to know T2, let's rearrange the first equation for T1:

Substituting this into the second equation, we get:

Rearranging for T2:

Using our given values, we can solve for T2:

This is the tension of the spring. There are two equatons that we can write out for the spring:

The only variables we don't know are  and , so we can solve these two equations simultaneously. We want , so let's rearrange the first equation for :

Substituting this into the second equation, we get:

Rearranging for :

We know the force and potential energy, allowing us to solve:

There is quite a lot going on in this problem. However, we will take it one step at a time so that you can understand the logical progression of thought it takes to solve this problem.

The first major step will be converting the frequency into a centripetal acceleration.

Convert the frequency into a velocity:

This is how fast the outer walls of the ride are traveling. We can convert this into centripetal acceleraton using the expression:

Then, we can create an expression for centripetal force for a student with mass :

Now that we have a term for the centirpetal force, we can work toward finding the force of friction. The centripetal force is also the normal force used in calculating frictional force. If the student is pinned to the wall, then the frictional force is exactly equal to the student's weight.

Plugging in our expression for the normal force:

Cancel out mass and rearrange for the coefficient of friction:

We are asked for the period of the pendulum, or the time it takes to make one full revolution or swing.

The period of a pendulum is given by this formula:

Where  and 

It takes roughly 12 seconds for the pendulum to make a full swing. Note that the mass attached to the end of the pendulum is irrelevant.

In this case, the kinetic energy of the spring is at a minimum. This is because, as the question indicates, the spring is not moving. At the same time, because the spring is compressed as far is it can be compressed, we know that its potential energy is at a maximum. The total energy of the spring therefore cannot be zero. 

The only factor that affects the period of a pendulum is the length of the pendulum. Therefore we can ignore any of the other answers which include other factors. The equation for the period of a pendulum is:

The center of mass is the point where we can consider all of the substance's mass to be concentrated. Finding the center of mass greatly facilitates mechanics problems, because we can perceive the force to be acting on only this one point.

Since the lead side of the cylinder is heavier than the aluminum side, we can conclude that the center of mass is located inside the lead side of the cylinder. Since the lead side has a mass of 60g, each inch of the lead side will have a mass of 15g. By going one inch into the lead side, there are 45g on each side of the point. As a result, we say that this is the location for the center of mass for the cylinder, as either side would weigh the same individually.