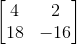All Linear Algebra Resources
Example Questions
Example Question #231 : Operations And Properties
Determine the inverse of matrix A where
The inverse for this matrix does not exist.
The matrix is square, so it could have an inverse. Next you need to find the determinant which is -6. Swap the numbers in spots a and d and put a negative in front of the numbers in spots b and c.

Example Question #231 : Operations And Properties
Determine the inverse of matrix A where
The inverse for this matrix does not exist.
The inverse for this matrix does not exist.
The matrix is square, so it could have an inverse. Next, calculate the determinant. The determinant for this matrix is 0 so it does not have an inverse.
Example Question #13 : The Inverse
Determine the inverse of matrix A where
This matrix does not have an inverse.
A matrix must be square to have an inverse. This matrix is square, so it could have an inverse. Next the determinant of the matrix must not be 0 to have an inverse. The determinant of this matrix is -6, so it has an inverse. To find the inverse of a 3x3 matrix, first write it in augmented form.
Next find the pivot in the first column by dividing R1/2.
Next, eliminate the first column by subtracting R2-5R1 and R3-2R1
Next, find the pivot in column 2 by dividing -7R2/2
Next, eliminate the second column by subtracting R1-3R2/2 and R3+2R2
Next find the pivot in column 3 by dividing 6R3/7
Finally, Eliminate the third column by subtracting R1-20R3/7 and R2-
Now that we have the identity matrix on the left side, the right side is our answer.
Example Question #232 : Operations And Properties
Determine the inverse of matrix A where
The inverse for this matrix does not exist.
The inverse for this matrix does not exist.
The matrix must be square to have an inverse. This matrix is square so it could have an inverse. A matrix must also have a non-zero determinant. The determinant for this matrix is zero, so it does not have an inverse.
Example Question #15 : The Inverse
Determine the inverse of matrix A where
This matrix does not have an inverse
To find the inverse of a matrix first look to verify that the matrix is square. If it is not square, it does not have an inverse. Next, you must find the determinant. If the determinant is 0, then the matrix does not have an inverse. The determinant for this matrix is ad-bc = 16, therefore it has an inverse. To find the inverse of a 2x2 matrix we first write it in augmented form.






Example Question #16 : The Inverse
Determine the inverse of matrix A where
Inverse does not exist
To determine the inverse of a matrix, you must first verify that the matrix is square. Next calculate the determinant. The determinant for this matrix is -2. Now you can swap the numbers in a and d and put a negative in front of the numbers in b and c. 
Example Question #17 : The Inverse
Determine the inverse of matrix A where
This matrix does not have an inverse.
The matrix is square, so it could have an inverse. Next you need to find the determinant which is 362. Swap the numbers in spots a and d and put a negative in front of the numbers in spots b and c.

Example Question #318 : Linear Algebra
True or false: A matrix with five rows and four columns has as its inverse a matrix with four rows and five columns.
False
True
False
Only a square matrix - a matrix with an equal number of rows and columns - has an inverse. Therefore, a matrix with five rows and four columns cannot even have an inverse.
Example Question #319 : Linear Algebra
True or false:
If a matrix with four rows and four columns has an inverse, then the inverse also has four rows and four columns.
False
True
True
The inverse of a square matrix - that is, a matrix with an equal number of rows and columns - if it exists, is equal in dimension to that matrix. Therefore, any inverse of a four-by-four matrix is itself a four-by-four matrix.
Example Question #241 : Operations And Properties


True or false: 
False
True
False
To prove a statement false, it suffices to find one case in which the statement does not hold. We show that

provide a counterexample.
A matrix is singular - that is, without an inverse - if and only if its determinant is equal to zero. The determinant of a two-by-two matrix is equal to the product of its upper left to lower right entries minus that of its upper right to lower left entries, so:
Both 

Now add the matrices by adding them term by term.
This is simply the two-by-two identity, which has an inverse - namely, itself.
The statement has been proved false by counterexample.
All Linear Algebra Resources