ISEE Upper Level Quantitative : Equilateral Triangles
Study concepts, example questions & explanations for ISEE Upper Level Quantitative
All ISEE Upper Level Quantitative Resources
Example Questions
Example Question #21 : Geometry
Which is the greater quantity?
(a) The perimeter of
(b) Twice the perimeter of
(a) is greater.
It is impossible to tell from the information given.
(a) and (b) are equal.
(b) is greater.
(a) and (b) are equal.
If segments are constructed in which the endpoints form the midpoints of the sides of a triangle, then each of the sides of the smaller triangle is half as long as the side of the larger triangle that it does not touch. Therefore:
The perimeter of 
which is twice the perimeter of 
Note that the fact that the triangle is equilateral is irrelevant.
Example Question #21 : Geometry
Column A Column B
The perimeter The perimeter
of a square with of an equilateral
sides of 4 cm. triangle with a side
of 9 cm.
The quantity in Column B is greater.
There is not enough info to determine a relationship between the columns.
The quantities in both columns are equal.
The quantity in Column A is greater.
The quantity in Column B is greater.
Perimeter involves adding up all of the sides of the shape. Therefore, the square's perimeter is 
Example Question #1 : How To Find The Area Of An Equilateral Triangle
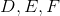
Which is the greater quantity?
(a) The area of
(b) Twice the area of
(b) is greater.
It is impossible to tell from the information given.
(a) is greater.
(a) and (b) are equal.
(a) is greater.
If segments are constructed in which the endpoints form the midpoints of the sides of a triangle, then four triangles, congruent to each other and similar to the larger triangle, are formed. Therefore, one of these triangles - specifically, 
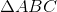
Note that the fact that the triangle is equilateral is irrelevant.
Example Question #1 : How To Find The Length Of The Side Of An Equilateral Triangle
Which of the following could be the three sidelengths of an equilateral triangle?
By definition, an equilateral triangle has three sides of equal length. We can identify the equilateral triangle by converting the given sidelengths to the same units and comparing them.
We can eliminate the following by showing that at least two sidelengths differ.
2 yards = 
Two sides have lengths 6 feet and 7 feet, so we can eliminate this choice.
4 feet = 
Two sides have lengths 48 inches and 50 inches, so we can eliminate this choice.
5 feet = 
Two sides have lengths 48 inches and 60 inches, so we can eliminate this choice.
Two sides have lengths 4 feet and 5 feet, so we can eliminate this choice.
All three sides have the same length, making this the triangle equilateral. This choice is correct.
Certified Tutor
All ISEE Upper Level Quantitative Resources
