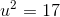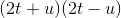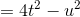We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Quantitative : Variables

Study concepts, example questions & explanations for ISEE Upper Level Quantitative

Create An Account

All ISEE Upper Level Quantitative Resources

8 Diagnostic Tests 234 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #861 : Isee Upper Level (Grades 9 12) Quantitative Reasoning

$t ^{2} = 40$

$u ^{2}= 17$

Evaluate (2t+u) (2t-u) .

Possible Answers:

177

143

Correct answer:

143

Explanation:

(2t+u) (2t-u) is the product of the sum and the difference of the same two binomials, so this can be rewritten, and evaluated, using the difference of squares pattern:

(2t+u) (2t-u)

$= (2 t)^{2} - u^{2}$

$= 2^{2} \cdot t ^{2} - u^{2}$

$= 4 t ^{2} - u^{2}$

= 4 (40 ) - 17

= 160 - 17

= 143

Report an Error

Example Question #1 : How To Divide Variables

The ratio of 10 to 14 is closest to what value?

Possible Answers:

0.04

0.24

0.71

0.57

Correct answer:

0.71

Explanation:

Another way to express ratios is through division. 10 divided by 14 is approximate 0.71.

Report an Error

Example Question #1 : How To Divide Variables

If is the quotient of and , which statement could be true?

Possible Answers:

p+v=q

$p\div q=v$

v-p=q

v p=q

$p\div \ v=q$

Correct answer:

$p\div \ v=q$

Explanation:

A quotient is the result of division. If is the quotient of and , that means that $p\div v=q$ could be true.

Report an Error

Example Question #2 : How To Divide Variables

is a negative integer. Which is the greater quantity?

(A) $A \div \left ( - \frac{1}{3}\right )$

(B) $A \div \left ( -0.3\right )$

Possible Answers:

(A) is greater

(A) and (B) are equal

It is impossible to tell which is greater from the information given

(B) is greater

Correct answer:

(B) is greater

Explanation:

Since the quotient of negative numbers is positive, both results will be positive.

We can rewrite both of these as products of positive numbers, as follows:

$A \div \left ( - \frac{1}{3}\right ) = \left | A \right | \div \frac{1}{3} = \left | A \right | \cdot 3$

$A \div \left ( -0.3\right ) =A \div \left ( - \frac{3}{10}\right ) = \left | A \right | \div \frac{3}{10} = \left | A \right | \cdot \frac{10}{3} = \left | A \right | \cdot 3 \frac{1}{3}$

$3 \frac{1}{3} > 3$ , so

$\left | A \right | \cdot 3 \frac{1}{3} >\left | A \right | \cdot 3$ , and

$A \div \left ( -0.3\right ) > A \div \left ( - \frac{1}{3}\right )$

making (B) greater.

Report an Error

Example Question #1 : How To Divide Variables

is a negative integer. Which is the greater quantity?

(A) $A \div (- \sqrt{5})$

(B) $A \div (- \sqrt{7})$

Possible Answers:

(A) and (B) are equal

(A) is greater

It is impossible to determine which is greater from the information given

(B) is greater

Correct answer:

(A) is greater

Explanation:

Since the quotient of negative numbers is positive, both results will be positive.

We can rewrite both of these as quotients of positive numbers, as follows:

$A \div (- \sqrt{5}) =\left | A \right | \div \sqrt{5}$

$A \div (- \sqrt{7}) =\left | A \right | \div \sqrt{7}$

Since the expressions have the same dividend and the second has the greater divisor, the first has the greater quotient.

Therefore, (A) is greater.

Report an Error

Example Question #2 : How To Divide Variables

Let be negative. Which of the following is the greater quantity?

(A) $y \div \left ( -8\right )$

(B) $y \div \left ( -7\right )$

Possible Answers:

It is impossible to determine which is greater from the information given

(A) is greater

(A) and (B) are equal

(B) is greater

Correct answer:

(B) is greater

Explanation:

The quotient of two negative numbers is positive. The expressions can be rewritten as follows:

$y \div \left ( -8\right ) = \left | y\right | \div 8$

$y \div \left ( -7\right ) = \left | y\right | \div 7$

Both expressions have the same dividend; the second has the lesser divisor so it has the greater quotient. This makes (B) greater.

Report an Error

Example Question #6 : How To Divide Variables

When evaluating the expression

$a+ b \cdot c \div \left ( d ^{2}- e \right )$ ,

assuming you know the values of all five variables, what is the second operation that must be performed?

Possible Answers:

Squaring

Addition

Subtraction

Multiplication

Division

Correct answer:

Subtraction

Explanation:

In the order of operations, any expression within parentheses must be performed first. Between the parentheses, there are two operations, an exponentiation (squaring), and a subtraction. By the order of operations, the exponentiation is performed first; the subtraction is performed second, making this the correct response.

Report an Error

Example Question #7 : How To Divide Variables

is a negative number.

Which is the greater quantity?

(a) The reciprocal of

(b) The reciprocal of

Possible Answers:

(a) is the greater quantity

(b) is the greater quantity

It is impossible to determine which is greater from the information given

(a) and (b) are equal

Correct answer:

(b) is the greater quantity

Explanation:

Since is negative, its reciprocal $\frac{1}{x}$ is also negative. Since

$1 > \frac{1}{2}$ ,

by the Multiplication Property of Inequality,

$1 \cdot \frac{1}{x}< \frac{1}{2}\cdot \frac{1}{x}$

$\frac{1}{x}< \frac{1}{2 \cdot x}$

$\frac{1}{x}< \frac{1}{2 x}$

That is, the reciprocal of is greater than that of .

Report an Error

Example Question #8 : How To Divide Variables

0 < |x |< 1 ; $x \ne 0$ .

Which is the greater quantity?

(a) The reciprocal of

(b) The reciprocal of x + 2

Possible Answers:

(b) is the greater quantity

It is impossible to determine which is greater from the information given

(a) is the greater quantity

(a) and (b) are equal

Correct answer:

It is impossible to determine which is greater from the information given

Explanation:

We show that the given information is insufficient by examining two cases.

Case 1:

$x = -\frac{1}{2}$

The reciprocal of is $- \frac{2} {1}$ , or .

Also, $x + 2 = -\frac{1}{2} + 2 = 1 \frac{1}{2} = \frac{3}{2}$ , the reciprocal of which is $\frac{2}{3}$ .

$\frac{2}{3} > -\frac{1}{2}$ , so (b) is the greater quantity.

Case 2: $x = \frac{1}{2}$ .

The reciprocal of is $\frac{2} {1}$ , or 2.

Also, $x + 2 = \frac{1}{2} + 2 =2 \frac{1}{2} = \frac{5}{2}$ , the reciprocal of which is $\frac{2}{5}$ .

$2 > \frac{2}{5}$ , so (a) is the greater quantity.

|x| < 1 in both cases, but in one case, (a) is greater and in the other, (b) is greater.

Report an Error

Example Question #1 : How To Subtract Variables

Simplify:

5y + 4x - 8y - 12y

Possible Answers:

4x-15y

9x-20y

9x-4y

4x-25y

9x + 4y

Correct answer:

4x-15y

Explanation:

5y + 4x - 8y - 12y

$= 4x + \left (5 - 8 - 12 \right ) y$

$= 4x + \left (-3 - 12 \right ) y$

$= 4x + \left (-15 \right ) y$

=4x - 15y

Report an Error

View Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View Tutors

Ana
Certified Tutor

Grand Canyon University, Bachelors, Education. Grand Canyon University, Masters, Education.

View Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

All ISEE Upper Level Quantitative Resources

8 Diagnostic Tests 234 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Atlanta, Statistics Tutors in Dallas Fort Worth, Physics Tutors in Dallas Fort Worth, Algebra Tutors in Los Angeles, Statistics Tutors in Atlanta, ACT Tutors in Boston, Algebra Tutors in New York City, English Tutors in Los Angeles, LSAT Tutors in Denver, Spanish Tutors in Boston

Popular Courses & Classes

GMAT Courses & Classes in New York City, ACT Courses & Classes in New York City, LSAT Courses & Classes in Phoenix, SAT Courses & Classes in Chicago, SSAT Courses & Classes in New York City, SSAT Courses & Classes in Boston, SSAT Courses & Classes in Miami, SAT Courses & Classes in New York City, Spanish Courses & Classes in Houston, ACT Courses & Classes in Philadelphia

Popular Test Prep

GMAT Test Prep in Philadelphia, SAT Test Prep in San Diego, ACT Test Prep in New York City, GMAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Boston, ISEE Test Prep in San Francisco-Bay Area, ACT Test Prep in Philadelphia, ACT Test Prep in Atlanta, ACT Test Prep in San Diego, GMAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Quantitative : Variables

Study concepts, example questions & explanations for ISEE Upper Level Quantitative

All ISEE Upper Level Quantitative Resources

Example Questions

Example Question #861 : Isee Upper Level (Grades 9 12) Quantitative Reasoning

Example Question #1 : How To Divide Variables

Example Question #1 : How To Divide Variables

Example Question #2 : How To Divide Variables

Example Question #1 : How To Divide Variables

Example Question #2 : How To Divide Variables

Example Question #6 : How To Divide Variables

Example Question #7 : How To Divide Variables

Example Question #8 : How To Divide Variables

Example Question #1 : How To Subtract Variables

All ISEE Upper Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: