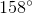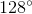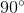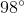All ISEE Upper Level Math Resources
Example Questions
Example Question #10 : Lines
A line 






Evaluate 
When a transversal such as 
Two same-side interior angles are supplementary - that is, their angle measures total 180 - so
We can solve this system by the substitution method as follows:
Backsolve:

Example Question #262 : Geometry

Note: Figure NOT drawn to scale.
Refer to the above diagram. Give the measure of 
The top and bottom angles, being vertical angles - angles which share a vertex and whose union is a pair of lines - have the same measure, so

or, simplified,
The right and bottom angles form a linear pair, so their degree measures total 180. That is,
Substitute 

The left and right angles, being vertical angles, have the same measure, so, since the right angle measures 

Example Question #41 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Figure NOT drawn to scale
The above figure shows Trapezoid 




By the Same-Side Interior Angle Theorem, since 






The corresponding major arc, 
The measure of an angle formed by two tangents to a circle is equal to half the difference of those of its intercepted arcs:
Again, by the Same-Side Interior Angles Theorem, 

Example Question #41 : Plane Geometry
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to 

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Isosceles Triangle
The triangles are similar. Solve for 

Because the triangles are similar, proportions can be used to solve for the length of the side:
Cross-multiply:
Example Question #41 : Geometry
One of the base angles of an isosceles triangle is 
The base angles of an isosceles triangle are always equal. Therefore both base angles are 
Let 
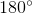
Example Question #41 : Geometry
A right triangle has a hypotenuse of 10 and a side of 6. What is the missing side?
To find the missing side, use the Pythagorean Theorem 



Example Question #3 : Triangles

Refer to the above diagram. Which of the following quadratic equations would yield the value of 
By the Pythagorean Theorem,
Example Question #2 : Right Triangles

Note: Figure NOT drawn to scale.
Refer to the above diagram. Which of the following quadratic equations would yield the value of 
By the Pythagorean Theorem,
Example Question #2 : Triangles

Note: Figure NOT drawn to scale.
Refer to the above diagram.
Find the length of 
First, find 
Since 


Certified Tutor
Certified Tutor
All ISEE Upper Level Math Resources