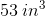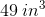We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : Solid Geometry

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 … 12 13 Next →

Example Question #3 : How To Find The Volume Of A Pyramid

A right regular pyramid with volume 1,000 has its vertices at the points

(0,0,0), (n,0, 0), (n,n,0), (0, n, n), (n,n,n)

where n > 0 .

Evaluate .

Possible Answers:

n = 10

n = 30

$n = 10 \sqrt[3]{2}$

$n = 10 \sqrt[3]{3 }$

n = 20

Correct answer:

$n = 10 \sqrt[3]{3 }$

Explanation:

The pyramid has a square base that is units by units, and its height is units, as can be seen from this diagram,

Pyramid

The square base has area $B = n^{2}$ ; the pyramid has volume $V = \frac{1}{3} \cdot n^{2} \cdot n = \frac{1}{3} n^{3}$

Since the volume is 1,000, we can set this equal to 1,000 and solve for :

$\frac{1}{3} n^{3} = 1,000$

$n^{3} = 3,000$

$n = \sqrt[3]{3,000} = \sqrt[3]{1,000} \cdot \sqrt[3]{3 } = 10 \sqrt[3]{3 }$

Report an Error

Example Question #4 : How To Find The Volume Of A Pyramid

Find the volume of a pyramid with the following measurements:

length = 4in
width = 3in
height = 5in

Possible Answers:

$80\text{in}^3$

$12\text{in}^3$

$20\text{in}^3$

$40\text{in}^3$

$60\text{in}^3$

Correct answer:

$20\text{in}^3$

Explanation:

To find the volume of a pyramid, we will use the following formula:

$V = \frac{l \cdot w \cdot h}{3}$

where l is the length, w is the width, and h is the height of the pyramid.

Now, we know the base of the pyramid has a length of 4in. We also know the base of the pyramid has a width of 3in. We also know the pyramid has a height of 5in.

Knowing this, we can substitute into the formula. We get

$V = \frac{4\text{in} \cdot 3\text{in} \cdot 5\text{in}}{3}$

$V = \frac{60\text{in}^3}{3}$

$V = 20\text{in}^3$

Report an Error

Example Question #5 : How To Find The Volume Of A Pyramid

Find the volume of a pyramid with the following measurements:

length = 4cm
width = 9cm
height = 8cm

Possible Answers:

$24\text{cm}^3$

$126\text{cm}^3$

$154\text{cm}^3$

$288\text{cm}^3$

$96\text{cm}^3$

Correct answer:

$96\text{cm}^3$

Explanation:

To find the volume of a pyramid, we will use the following formula:

$V = \frac{l \cdot w \cdot h}{3}$

where l is the length, w is the width, and h is the height of the pyramid.

Now, we know the following measurements:

length = 4cm
width = 9cm
height = 8cm

Knowing this, we can substitute into the formula. We get

$V = \frac{4\text{cm} \cdot 9\text{cm} \cdot 8\text{cm}}{3}$

$V = \frac{288\text{cm}^3}{3}$

$V = 96\text{cm}^3$

Report an Error

Example Question #6 : How To Find The Volume Of A Pyramid

Find the volume of a pyramid with the following measurements:

length: 7in
width: 6in
height: 8in

Possible Answers:

$336\text{in}^3$

$426\text{in}^3$

$168\text{in}^3$

$221\text{in}^3$

$112\text{in}^3$

Correct answer:

$112\text{in}^3$

Explanation:

To find the volume of a pyramid, we will use the following formula:

$V = \frac{lwh}{3}$

where l is the length, w is the width, and h is the height of the pyramid.

Now, we know the following measurements:

length: 7in
width: 6in
height: 8in

So, we get

$V = \frac{ 7\text{in} \cdot 6\text{in} \cdot 8\text{in}}{3}$

$V = \frac{42\text{in}^2 \cdot 8\text{in}}{3}$

$V = \frac{336\text{in}^3}{3}$

$V = 112\text{in}^3$

Report an Error

Example Question #11 : Solid Geometry

Find the volume of a pyramid with the following measurements: length= in, width= in, height= in

Possible Answers:

$221\text{in}^3$

$168\text{in}^3$

$336\text{in}^3$

$426\text{in}^3$

$112\text{in}^3$

Correct answer:

$112\text{in}^3$

Explanation:

To find the volume of a pyramid, we will use the following formula:

$V = \frac{lwh}{3}$

where l is the length, w is the width, and h is the height of the pyramid.

Now, we know the following measurements:

length: 7in
width: 6in
height: 8in

So, we get

$V = \frac{ 7\text{in} \cdot 6\text{in} \cdot 8\text{in}}{3}$

$V = \frac{42\text{in} \cdot 8\text{in}}{3}$

$V = \frac{336\text{in}}{3}$

$V = 112\text{in}^3$

Report an Error

Example Question #1 : Finding Volume Of A Cube

If a cube is inches tall, what is its volume?

Possible Answers:

500

384

Not enough information provided.

512

Correct answer:

512

Explanation:

To find the volume of a cube, we multiply length by width by height, which can be represented with the forumla $v=l\cdot w\cdot h$ . Since a cube has equal sides, we can use for all three values.

$8\cdot 8\cdot 8=512\: in ^{3}$

Report an Error

Example Question #61 : Volume

What is the volume of a cube with a side length equal to inches?

Possible Answers:

$53\: in^{3}$

$343\: in^{3}$

$21\: in^{3}$

$49\: in^{3}$

Correct answer:

$343\: in^{3}$

Explanation:

The volume of a a cube (or rectangular prism) can be solved using the following equation:

$V=l\times\ w\times\ h$

$V=7in\times 7in\times 7in=343in^3$

Report an Error

Example Question #1 : How To Find The Volume Of A Cube

Give the volume of a cube with surface area 150 square inches.

Possible Answers:

$375\textup{ in}^{3}$

$125\textup{ in}^{3}$

$125\sqrt{3}\textup{ in}^{3}$

$250\textup{ in}^{3}$

$250\sqrt{3}\textup{ in}^{3}$

Correct answer:

$125\textup{ in}^{3}$

Explanation:

Let be the length of one edge of the cube. Since its surface area is 150 square inches, one face has one-sixth of this area, or $\frac{150}{6} = 25$ square inches. Therefore, $s^{2} = 25$ , and s = 5 .

The volume is the cube of this, or $V= 5^{3}=125$ cubic inches.

Report an Error

Example Question #1 : How To Find The Volume Of A Cube

What is the volume of a cube in which the edge is equal to $\sqrt[3]{x}$ , and the value of is:

$x=5(4+3^{2})-3$

Possible Answers:

Correct answer:

Explanation:

First, the value of x must be solved for:

$x=5(4+3^{2})-3$

x=5(4+9)-3

x=5(13)-3

x=62

Given the edge of the cube is $\sqrt[3]{x}$ , plugging in the value of x results in $\sqrt[3]{62}$ . Thus, the area would be equal to this value cubed, which would result in 62.

Thus, 62 is the correct answer.

Report an Error

Example Question #1 : How To Find The Volume Of A Cube

The length of a diagonal of one face of a cube is . Give the volume of the cube.

Possible Answers:

$\frac{N^{3} \sqrt{2} }{4}$

$\frac{N^{3} \sqrt{2} }{2}$

$\frac{N^{3} \sqrt{3} }{3}$

$\frac{N^{3} \sqrt{3} }{9}$

$3N^{3}$

Correct answer:

$\frac{N^{3} \sqrt{2} }{4}$

Explanation:

Since a diagonal of a square face of the cube is, each side of each square has length $\frac{N}{\sqrt{2}}=\frac{N\sqrt{2}}{2}$ .

Cube this to get the volume of the cube:

$\left (\frac{N\sqrt{2}}{2} \right )^{3}$

$= \frac{N^{3}\left ( \sqrt{2} \right )^{3} }{2^{3} }$

$= \frac{N^{3} \cdot 2 \sqrt{2} }{8}$

$= \frac{N^{3} \sqrt{2} }{4}$

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 … 12 13 Next →

View Tutors

Lazaro
Certified Tutor

Miami Dade College, Bachelor of Engineering, Computer Hardware Engineering.

View Tutors

Aaron
Certified Tutor

Portland State University, Bachelors, Economics. Portland State University, Masters, Environmental and Resource Management.

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in New York City, Biology Tutors in Philadelphia, Computer Science Tutors in New York City, ISEE Tutors in Philadelphia, SAT Tutors in Atlanta, Statistics Tutors in Denver, ISEE Tutors in Seattle, Physics Tutors in Boston, LSAT Tutors in Washington DC, Biology Tutors in Denver

Popular Courses & Classes

ISEE Courses & Classes in San Diego, GRE Courses & Classes in Denver, Spanish Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Houston, SAT Courses & Classes in Phoenix, GRE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Miami, Spanish Courses & Classes in Houston, GRE Courses & Classes in Phoenix, GMAT Courses & Classes in Miami

Popular Test Prep

ISEE Test Prep in San Diego, LSAT Test Prep in Atlanta, ISEE Test Prep in Houston, MCAT Test Prep in New York City, SSAT Test Prep in San Diego, ACT Test Prep in Phoenix, MCAT Test Prep in Phoenix, ACT Test Prep in Houston, ISEE Test Prep in Los Angeles, GMAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : Solid Geometry

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #3 : How To Find The Volume Of A Pyramid

Example Question #4 : How To Find The Volume Of A Pyramid

Example Question #5 : How To Find The Volume Of A Pyramid

Example Question #6 : How To Find The Volume Of A Pyramid

Example Question #11 : Solid Geometry

Example Question #1 : Finding Volume Of A Cube

Example Question #61 : Volume

Example Question #1 : How To Find The Volume Of A Cube

Example Question #1 : How To Find The Volume Of A Cube

Example Question #1 : How To Find The Volume Of A Cube

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: