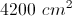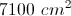Intermediate Geometry : Circles
Study concepts, example questions & explanations for Intermediate Geometry
All Intermediate Geometry Resources
Example Questions
Example Question #7 : How To Find The Percentage Of A Sector From An Angle
A survey was given to 300 local townspeople regarding their favorite local dish. The results of the survey are below, with the number of degrees of each sector representing each dish following.
Fried chicken, 87 degrees
Steak and potatoes, 75 degrees
Corned beef hash, 82 degrees
Chicken enchiladas, 94 degrees
Bison burger, 22 degrees
What percent of the local townspeople prefer a dish that includes chicken?
First add together the number of degrees of both sectors representing a dish with chicken (fried chicken and chicken enchiladas), 87 + 94.
Then set-up a proportion with this sum:
Example Question #2 : How To Find The Percentage Of A Sector From An Angle
A pie chart represents the ages of children in a local basketball league. The data is shown below, with the age range of each sector followed by the number of degrees of that sector.
Ages 2-4, 20 degrees
Ages 5-7, 30 degrees
Ages 8-10, 100 degrees
Ages 11-13, 90 degrees
Ages 14-16, ? degrees
What percent of the children in the basketball league are between the ages of 14-16?
None of the other answers.
First add together the degrees of the sectors representing children ages 2-13. Then take that sum, 240 degrees, away from the total degrees of the circle, 360 degrees.
Finally set-up a proportion with the remaining degrees (120) which represents the sector of children ages 14-16.
Solve your proportion:
Example Question #9 : How To Find The Percentage Of A Sector From An Angle
A circle chart represents the survey results of the following question:
How many hours a week do you typically spend watching TV?
The results are below, with the sector title and the number of degrees of each sector following.
Less than 1 hour, 40 degrees
1-4 hours, 45 degrees
5-8 hours, 30 degrees
9-12 hours, 100 degrees
13-16 hours, 85 degrees
17 hours or more, 60 degrees
What percent of people surveyed watch TV for 9 or more hours a week?
First, add together the degrees from the 3 sectors that include 9 or more hours of TV: 100 degrees, 85 degrees and 60 degrees.
Take this sum, 245 degrees, and set-up a proportion:
Example Question #1 : How To Find The Percentage Of A Sector From An Angle
A circle graph represents the demographics of a major US city. The data is shown below with the category followed by the number of degrees making up that category's sector.
Black or African-American: 100 degrees
Hispanic or Latino: 100 degrees
White: 80 degrees
Two or more races: ? degrees
What percent of the city's population classifies themselves as being 2 or more races?
First, add together the degrees of the known sectors: 100 degrees, 100 degrees, and 80 degrees.
Subtract this sum (280 degrees) from the total number of degrees in a circle (360 degrees).
Take this difference to set-up a proportion:
Example Question #11 : How To Find The Percentage Of A Sector From An Angle
A survey was given to 1,000 middle school students across the United States, asking them to choose their favorite subject in school. The results of the survey are below, with each subject followed by the number of degrees composing that subject's sector in the circle graph displaying this data.
Math, 75 degrees
English, 58 degrees
Science, 62 degrees
Social Studies, 100 degrees
Music, Art or PE: 65 degrees
What percent of students prefer a subject that is not Music, Art or PE?
None of the other answers.
First, add together the degrees of the sectors representing Math, English, Science and Social Studies.
Take this sum, 295 and set-up a proportion:
Example Question #22 : Circles
Reference a map of major cities on the West Coast to help you with this question!
A survey was given to fans throughout the West Coast, asking them who their favorite team was. The results are below with the team name and the degrees making up the sector representing that team in a circle graph that displayed this data.
Team A: 123 degrees
Team B: 89 degrees
Team C: 36 degrees
Team D: 20 degrees
Other: 92 degrees
What percent of fans prefere Team A, C, or D?
First add together the degrees from the sectors representing Teams A, C, and D.
Take this sum, 179 and set-up a proportion:
Example Question #21 : Plane Geometry
A pie chart depicts the favorite beverages of high schoolers. Below is the data with the beverage and the number of degrees making up that beverage's sector.
Soda: 86 degrees
Diet Soda: 44 degrees
Water: 55 degrees
Juice: 99 degrees
Lemonade: 66 degrees
Other: ? degrees
What percent of high schoolers prefer a beverage that was not specifically listed as a choice?
None of the other answers.
First add together the known sectors. Use that sum (350 degrees) and subtract from the total number of degrees in a circle (360 degrees).
Take that difference and set-up a proportion:
Example Question #11 : How To Find The Percentage Of A Sector From An Angle
A circle graph displays data of the eye colors of a group of middle schoolers. The data is shown below with the eye color followed by the number of degrees composing that sector.
Brown: 208 degrees
Green: 20 degrees
Blue: 25 degrees
Hazel: 50 degrees
Other: 57 degrees
What percent of students have brown eyes?
None of the other answers.
Take the degrees representing the brown eye sector and set-up a proportion:
Example Question #24 : Circles
In the above diagram, 
The three interior angles of equilateral triangle 
of the circle.
Example Question #1 : How To Find The Area Of A Sector
Find the approximate area of the shaded portion of the figure.
The answer is approximately 
First, you would need to find the diameter of the circle. Use the Pythagorean Theorem to get
or
Since the diameter is 130, we divide by 2 to get 65 cm for our radius. Then the area of the circle is
Next we would find the area of each triangle:
and
Then we would subtract these from our answer above to get:
All Intermediate Geometry Resources
