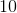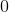Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : How to find the slope of a tangent line

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Tangent Lines

What is the slope of the tangent line to the graph of y=x^2-6 $\displaystyle y=x^2-6$ when x=3 $\displaystyle x=3$?

Possible Answers:

$\displaystyle 9$

$\displaystyle 6$

$\displaystyle 3$

$\displaystyle 0$

$\displaystyle 2$

Correct answer:

$\displaystyle 6$

Explanation:

To find the slope of the tangent line, first we must take the derivative of x^2-6 $\displaystyle x^2-6$, giving us $\displaystyle 2x$. Next we simply plug in our given x-value, which in this case is x=3 $\displaystyle x=3$. This leaves us with a slope of $\displaystyle 6$.

Report an Error

Example Question #11 : Tangent Lines

Suppose the equation of a line is $\displaystyle -3x+5y=-3$. What is the slope of the tangent line at x=3 $\displaystyle x=3$?

Possible Answers:

$-\frac{9}{5}$ $\displaystyle -\frac{9}{5}$

$\frac{9}{5}$ $\displaystyle \frac{9}{5}$

$\displaystyle -3$

$\frac{5}{3}$ $\displaystyle \frac{5}{3}$

$\frac{3}{5}$ $\displaystyle \frac{3}{5}$

Correct answer:

$\frac{3}{5}$ $\displaystyle \frac{3}{5}$

Explanation:

Rewrite $\displaystyle -3x+5y=-3$ in slope-intercept form, y=mx+b $\displaystyle y=mx+b$.

5y=3x-3 $\displaystyle 5y=3x-3$

$y=\frac{3}{5}x-\frac{3}{5}$ $\displaystyle y=\frac{3}{5}x-\frac{3}{5}$

The slope of the tangent line is $\frac{3}{5}$ $\displaystyle \frac{3}{5}$.

Report an Error

Example Question #221 : Coordinate Geometry

Suppose a function y=1 $\displaystyle y=1$. What is the slope of the tangent line at x=10 $\displaystyle x=10$?

Possible Answers:

$\displaystyle 0$

$\displaystyle -1$

$\displaystyle 10$

$\displaystyle 1$

$\textup{There is no slope.}$ $\displaystyle \textup{There is no slope.}$

Correct answer:

$\displaystyle 0$

Explanation:

Write the formula for slope-intercept form.

y=mx+b $\displaystyle y=mx+b$

m=0 $\displaystyle m=0$

The slope of y=1 $\displaystyle y=1$ is always zero at every point on the domain. Therefore, the slope at x=10 $\displaystyle x=10$ must also be zero.

Report an Error

View Tutors

Chris
Certified Tutor

U of Akron, Bachelors, Chemistry. YSU, Masters, Chemistry.

View Tutors

Julie
Certified Tutor

Université de Montréal, Professional (JD, MD, DMD, etc), Early Childhood.

View Tutors

Michael
Certified Tutor

Furman University, Bachelor in Arts, History. Covenant Theological Seminary, Master of Divinity, Theology.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Chicago, Chemistry Tutors in Miami, Computer Science Tutors in Atlanta, SAT Tutors in Washington DC, GRE Tutors in Seattle, Math Tutors in Philadelphia, Spanish Tutors in Dallas Fort Worth, French Tutors in New York City, MCAT Tutors in Boston, GMAT Tutors in Atlanta

Popular Courses & Classes

LSAT Courses & Classes in New York City, ACT Courses & Classes in Miami, SAT Courses & Classes in Denver, SSAT Courses & Classes in Miami, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in New York City, LSAT Courses & Classes in Chicago, SAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Denver, MCAT Courses & Classes in Atlanta

Popular Test Prep

SAT Test Prep in Philadelphia, MCAT Test Prep in Miami, SSAT Test Prep in New York City, SSAT Test Prep in Denver, LSAT Test Prep in Dallas Fort Worth, ACT Test Prep in Phoenix, SSAT Test Prep in Phoenix, SSAT Test Prep in Chicago, LSAT Test Prep in Philadelphia, GMAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : How to find the slope of a tangent line

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #2 : Tangent Lines

Example Question #11 : Tangent Lines

Example Question #221 : Coordinate Geometry

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: