Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : How to find the area of a pentagon

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Area Of A Pentagon

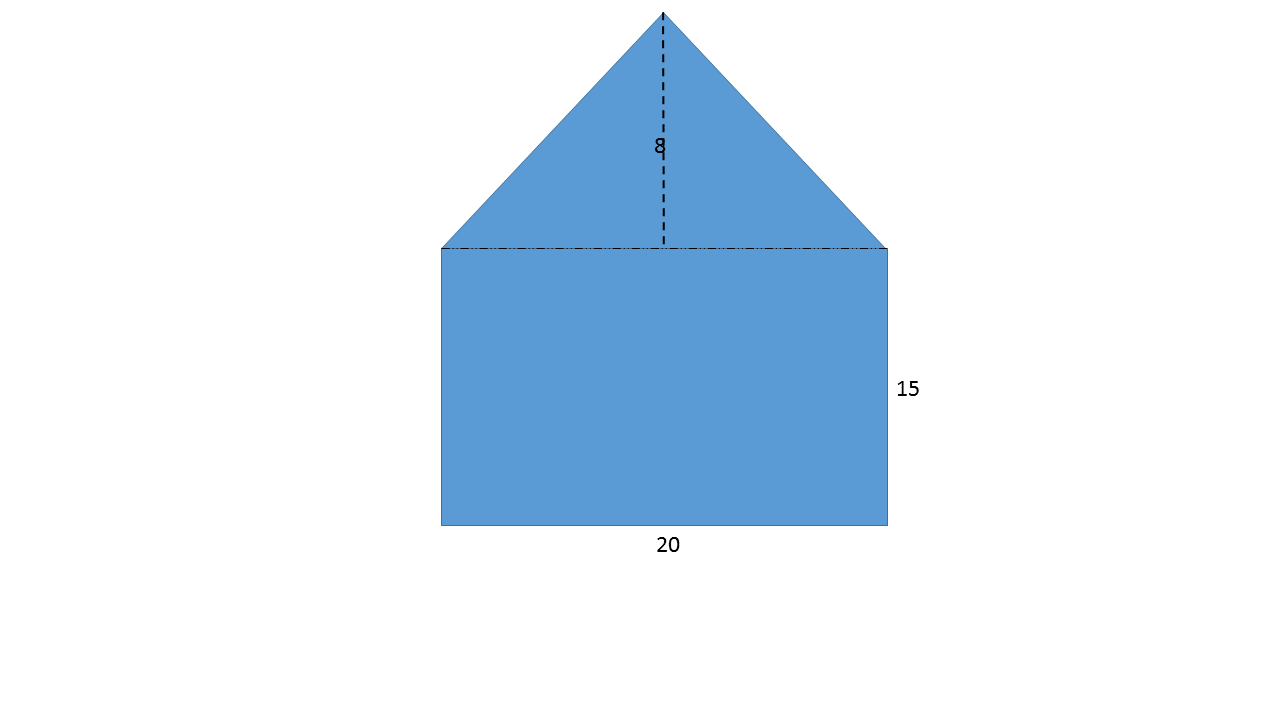
Pentagon_series_vt_custom_

Find the area of the pentagon shown above.

Possible Answers:

380 square units

340 square units

300 square units

320 square units

390 square units

Correct answer:

380 square units

Explanation:

To find the area of this pentagon, divide the interior of the pentagon into a four-sided rectangle and two right triangles. The area of the bottom rectangle can be found using the formula:

$A=width\times length$

$A=20\times15=300$

The area of the two right triangles can be found using the formula:

$A=\frac{base\times height}{2}$

$A=\frac{10\times 8}{2}=\frac{80}{2}=40$

Since there are two right triangles, the sum of both will equal the area of the entire triangular top portion of the pentagon.

Thus, the solution is:

A=300+40+40=380

Report an Error

Example Question #781 : Intermediate Geometry

Pentagon_series_vt_custom_

Find the area of the pentagon shown above.

Possible Answers:

416 square units

502 square units

672 square units

572 square units

Correct answer:

572 square units

Explanation:

To find the area of this pentagon, divide the interior of the pentagon into a four-sided rectangle and two right triangles. The area of the bottom rectangle can be found using the formula:

$A=width\times length$

$A=26\times16=416$

The area of the two right triangles can be found using the formula:

$A=\frac{base\times height}{2}$

$A=\frac{13\times 12}{2}=\frac{156}{2}=78$

Since there are two right triangles, the sum of both will equal the area of the entire triangular top portion of the pentagon.

Thus, the solution is:

A=416+78+78=572

Report an Error

Example Question #782 : Intermediate Geometry

A regular pentagon has a side length of inches and an apothem length of 6.2 inches. Find the area of the pentagon.

Possible Answers:

118 inches^2

inches^2

139.5 inches^2

inches^2

Correct answer:

139.5 inches^2

Explanation:

By definition a regular pentagon must have equal sides and equivalent interior angles. Since we are told that this pentagon has a side length of inches, all of the sides must have a length of inches. Additionally, the question provides the length of the apothem of the pentagon--which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of 6.2 .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{9\times 6.2}{2}=\frac{55.8}{2}=27.9$

Note: the area shown above is only the a measurement from one of the five total interior triangles. Thus, to find the total area of the pentagon multiply:

$27.9\times5=139.5$

Report an Error

Example Question #783 : Intermediate Geometry

A regular pentagon has a side length of and an apothem length of 9.6 . Find the area of the pentagon.

Possible Answers:

square units

200 square units

336 square units

67.2 square units

Correct answer:

336 square units

Explanation:

By definition a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon--which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of 9.6 .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{14\times 9.6}{2}=\frac{134.4}{2}=67.2$

Note: 67.2 is only the measurement for one of the five interior triangles. Thus, the final solution is:

$67.2\times5=336$

Report an Error

Example Question #784 : Intermediate Geometry

A regular pentagon has a perimeter of yards and an apothem length of 8.3 yards. Find the area of the pentagon.

Possible Answers:

249 yards^2

yards^2

200 yards^2

yards^2

248 yards^2

Correct answer:

249 yards^2

Explanation:

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:

p=5(s)

60=5(s)

$s=\frac{60}{5}=12$

Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of 8.3 .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{8.3\times 12}{2}=\frac{99.6}{2}=49.8$

Thus, the area of the entire pentagon is:

$A=49.8\times 5=249$

Report an Error

Example Question #785 : Intermediate Geometry

A regular pentagon has a side length of and an apothem length of 10.3 . Find the area of the pentagon.

Possible Answers:

306.25 square units

400.5 square units

383.5 square units

386.25 square units

270 square units

Correct answer:

386.25 square units

Explanation:

By definition a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of 10.3 .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{15\times 10.3}{2}=\frac{154.5}{2}=77.25$

Keep in mind that this is the area for only one of the five total interior triangles.

The total area of the pentagon is:

$A=77.25\times 5=386.25$

Report an Error

Example Question #786 : Intermediate Geometry

A regular pentagon has a perimeter of and an apothem length of . Find the area of the pentagon.

Possible Answers:

175 square units

135 square units

square units

170 square units

Correct answer:

175 square units

Explanation:

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:

p=5(s)

50=5(s)

$s=\frac{50}{5}=10$

Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{10\times 7}{2}=\frac{70}{2}=35$

To find the total area of the pentagon multiply:

$35\times5=175$

Report an Error

Example Question #2 : How To Find The Area Of A Pentagon

A regular pentagon has a side length of and an apothem length of 17.2 . Find the area of the pentagon.

Possible Answers:

900 square units

1,350 square units

1,075 square units

215 square units

725 square units

Correct answer:

1,075 square units

Explanation:

By definition a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of 17.2 .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{25\times 17.2}{2}=\frac{430}{2}=215$

However, the total area of the pentagon is equal to:

$215\times 5= 1,075$

Report an Error

Example Question #3 : How To Find The Area Of A Pentagon

A regular pentagon has a side length of and an apothem length of 4.8 . Find the area of the pentagon.

Possible Answers:

sq. units

16.8 sq. units

133.6 sq. units

33.6 sq. units

sq. units

Correct answer:

sq. units

Explanation:

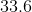
By definition a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of 4.8 .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{7\times 4.8}{2}=\frac{33.6}{2}=16.8$

Note: 16.8 is only the measurement for one of the five interior triangles. Thus, the solution is:

$16.8\times5=84$

Report an Error

Example Question #4 : How To Find The Area Of A Pentagon

A regular pentagon has a perimeter of and an apothem length of 8.9 . Find the area of the pentagon.

Possible Answers:

280.50

57.85

289.25

275.85

Correct answer:

289.25

Explanation:

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:

p=5(s)

65=5(s)

$s=\frac{65}{5}=13$

Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of 8.9 .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{8.9\times 13}{2}=\frac{115.7}{2}=57.85$

Thus, the area of the entire pentagon is:

$A=57.85\times 5=289.25$

Report an Error

View Tutors

Richard
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Chemistry. CUNY Brooklyn College, Master of Arts, Experimental Psychology.

View Tutors

Amin
Certified Tutor

Arcadia University, Bachelor in Arts, International Relations.

View Tutors

Liliana
Certified Tutor

Universidad del Caribe, Bachelor in Business Administration, Business, General.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Miami, Reading Tutors in Dallas Fort Worth, Biology Tutors in Miami, English Tutors in Houston, Chemistry Tutors in New York City, Computer Science Tutors in Phoenix, ISEE Tutors in Boston, Reading Tutors in Philadelphia, Calculus Tutors in Denver, Computer Science Tutors in Washington DC

Popular Courses & Classes

LSAT Courses & Classes in Boston, SAT Courses & Classes in Washington DC, GRE Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Houston, GMAT Courses & Classes in Boston, LSAT Courses & Classes in Houston, SAT Courses & Classes in Los Angeles, Spanish Courses & Classes in San Diego, GMAT Courses & Classes in New York City

Popular Test Prep

MCAT Test Prep in New York City, SAT Test Prep in Washington DC, GMAT Test Prep in Boston, ISEE Test Prep in San Diego, SAT Test Prep in Los Angeles, ISEE Test Prep in Los Angeles, SAT Test Prep in Philadelphia, ACT Test Prep in Phoenix, SAT Test Prep in Chicago, MCAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : How to find the area of a pentagon

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1 : How To Find The Area Of A Pentagon

Example Question #781 : Intermediate Geometry

Example Question #782 : Intermediate Geometry

Example Question #783 : Intermediate Geometry

Example Question #784 : Intermediate Geometry

Example Question #785 : Intermediate Geometry

Example Question #786 : Intermediate Geometry

Example Question #2 : How To Find The Area Of A Pentagon

Example Question #3 : How To Find The Area Of A Pentagon

Example Question #4 : How To Find The Area Of A Pentagon

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: