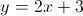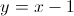All Intermediate Geometry Resources
Example Questions
Example Question #19 : Other Lines
Which of the following points is on the line 
Start by rewriting the equation into slope-intercept form.
To find which point is on the line, take the 



Plugging in 
Thus, 
Example Question #20 : Other Lines
Which of the following points is found on the line 
Start by rewriting the equation into slope-intercept form.
To find which point is on the line, take the 



Plugging in 
Thus, 
Example Question #21 : Other Lines
Which of the following points is on the line 
Start by rewriting the equation into slope-intercept form.
To find which point is on the line, take the 



Plugging in 
Thus, 
Example Question #1372 : Intermediate Geometry
Which of the following points is on the line 
Start by rewriting the equation into slope-intercept form.
To find which point is on the line, take the 



Plugging in 
Thus, 
Example Question #1373 : Intermediate Geometry
Which of the following points is found on the line 
Start by rewriting the equation into slope-intercept form.
To find which point is on the line, take the 



Plugging in 
Thus, 
Example Question #91 : Lines
True or false:
The line of the equation 

False
True
False
A line of an equation passes through the point with coordinates 




The line does not pass through the point.
Example Question #92 : Lines
True or false:
The line of the equation 
True
False
True
The coordinates of the origin are 



The statement is true, so the line does pass through the origin.
Example Question #24 : How To Find Out If A Point Is On A Line With An Equation
True or false:
The lines of the equations
and
intersect at the point 
(Note: You are given that the lines are distinct)
False
True
False
If two distinct lines intersect at the point 


Examine the second equation:
False; 
Therefore, the lines cannot intersect at 
Example Question #1 : How To Find The Equation Of A Line
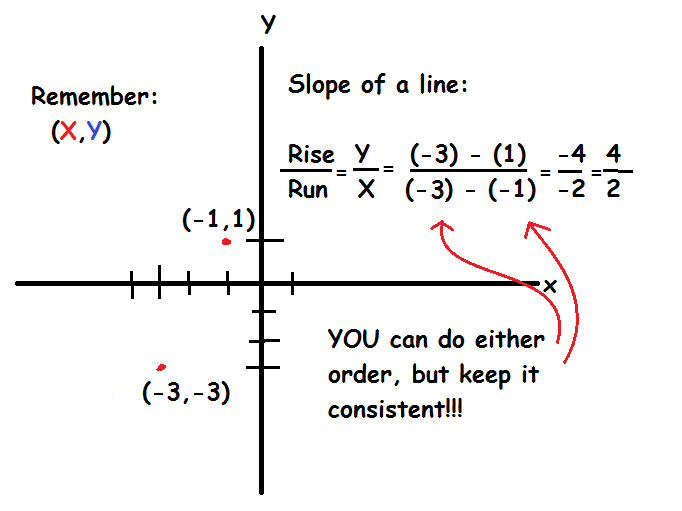
Given two points 

If we have two points, we can find the slope of the line between them by using the definition of the slope:

Now that we have our slope ( 




In order to find the y-intercept, we simply plug in one of the points on our line
So our equation looks like
Example Question #2 : How To Find The Equation Of A Line
Which of the following is an equation for a line with a slope of 

Because we have the desired slope and the y-intercept, we can easily write this as an equation in slope-intercept form (y=mx+b).
This gives us 


Certified Tutor
All Intermediate Geometry Resources