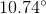All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Angle Of A Sector
What is the angle of a sector of area 


To begin, you should compute the complete area of the circle:
For your data, this is:
Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:
Now, multiply this by the total 
Rounded, this is 
Example Question #1 : How To Find The Angle Of A Sector
What is the angle of a sector that has an arc length of 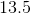



The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:
For your data, this means,
Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:
Rounded to the nearest hundredth, this is 
Example Question #101 : Sectors
What is the sector angle, in degrees, if the area of the sector is 

Write the formula for the area of a circular sector.
Substitute the given information and solve for theta:
Example Question #101 : Plane Geometry
The length of the intercepted arc of a sector of a circle with radius 

The formula for the length of an arc is
where 

Therefore, our central angle has a measure of
Example Question #102 : Sectors
A sector in a circle with a radius of 

Recall how to find the area of a sector:
Since the question asks for the measurement of the central angle, rearrange the equation like thus:
Plug in the given information to find the measurement of the central angle.
The central angle is 
Example Question #103 : Sectors
A sector in a circle with a radius of 

Recall how to find the area of a sector:
Since the question asks for the measurement of the central angle, rearrange the equation like thus:
Plug in the given information to find the measurement of the central angle.
The central angle is 
Example Question #104 : Sectors
A sector in a circle with a radius of 

Recall how to find the area of a sector:
Since the question asks for the measurement of the central angle, rearrange the equation like thus:
Plug in the given information to find the measurement of the central angle.
The central angle is 
Example Question #105 : Sectors
A sector in a circle with a radius of 

Recall how to find the area of a sector:
Since the question asks for the measurement of the central angle, rearrange the equation like thus:
Plug in the given information to find the measurement of the central angle.
The central angle is 
Example Question #8 : How To Find The Angle Of A Sector
A sector in a circle with a radius of 

Recall how to find the area of a sector:
Since the question asks for the measurement of the central angle, rearrange the equation like thus:
Plug in the given information to find the measurement of the central angle.
The central angle is 
Example Question #106 : Sectors
A sector in a circle with a radius of 

Recall how to find the area of a sector:
Since the question asks for the measurement of the central angle, rearrange the equation like thus:
Plug in the given information to find the measurement of the central angle.
The central angle is 
All Intermediate Geometry Resources