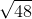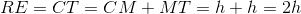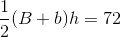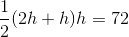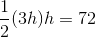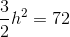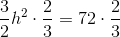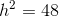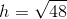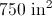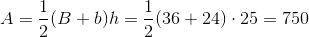Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1231 : Concepts

If a square has a side that is 3 yards long, what is the area in square feet?

Possible Answers:

$21\ \text{ft}^2$

$27\ \text{ft}^2$

$81\ \text{ft}^2$

$9\ \text{ft}^2$

$30\ \text{ft}^2$

Correct answer:

$81\ \text{ft}^2$

Explanation:

The area of a square is found by multiplying the length of a side by itself.

$A=s\times s=s^2$

If one side is 3 yards, this means one side is 9 feet since there are 3 feet in a yard.

$3\ \text{yards}\times3\ \text{feet per yard}=9\ \text{feet}$

Since every side is of equal length, you would multiply 9 feet by 9 feet to find the area.

$A=s\times s$

s=9

$A=9\times9=81$

This results in 81 square feet, which is the correct answer.

Report an Error

Example Question #1232 : Concepts

Find the perimeter of the trapezoid:
Question_12

Possible Answers:

$\small 21$

$\small 23.5$

$\small 26$

$\small 40$

Correct answer:

$\small 21$

Explanation:

The perimeter of any shape is equal to the sum of the lengths of its sides:

$\small P=4+6+3+8=21$

Report an Error

Example Question #41 : Geometry

The perimeter of a square is . Find the area.

Possible Answers:

484

444

7744

424

Correct answer:

484

Explanation:

A square has four equal sides. Given the value of the perimeter, divide the perimeter by four to determine each side length.

$\frac{88}{4}=22$

Square the side length to find the area since the area of the square is s^2 .

22^2 = 484

Report an Error

Example Question #1231 : Concepts

Find the area of a square in $\textup{inches}^{2}$ with a side length of $2\textup{ feet}$ .

Possible Answers:

$4\textup{ inches}^{2}$

$48\textup{ inches}^{2}$

$24\textup{ inches}^{2}$

$576\textup{ inches}^{2}$

$144\textup{ inches}^{2}$

Correct answer:

$576\textup{ inches}^{2}$

Explanation:

Write the area for a square.

A=s^2

Convert $\textup{2 feet}$ to inches first. One foot is $\textup{12 inches}$ .

$2 \textup{ feet}(\frac{12\textup{ inches}}{1\textup{ foot}}) = 24\textup{ inches}$

Substitute the side.

$A=(24 \textup{ inches})^2 = 576\textup{ inches}^2$

Report an Error

Example Question #11 : Triangles

The hypotenuse of a right triangle is feet; it has one leg feet long. Give its area in square inches.

Possible Answers:

$38,880 \textrm{ in}^{2}$

$43,120 \textrm{ in}^{2}$

$42,120 \textrm{ in}^{2}$

$77,760 \textrm{ in}^{2}$

$101,088 \textrm{ in}^{2}$

Correct answer:

$38,880 \textrm{ in}^{2}$

Explanation:

The area of a right triangle is half the product of the lengths of its legs, so we need to use the Pythagorean Theorem to find the length of the other leg. Set c = 39 , b = 36 :

$a^{2} = c^{2} - b^{2}$

$a^{2} = 39 ^{2} - 36^{2}$

$a^{2} = 1,521 - 1,296$

$a^{2} = 225$

$a = \sqrt{225} = 15$

The legs have length and feet; multiply both dimensions by to convert to inches:

$15 \times 12 = 180$ inches

$36 \times 12 = 432$ inches.

Now find half the product:

$A = \frac{1}{2} \cdot 180 \cdot 432 = 38,880\ in^{2}$

Report an Error

Example Question #161 : Geometry

Which of the following is equal to the area of a rectangle with length 4.3 meters and width 3.5 meters?

Possible Answers:

$15,500 \textrm{ cm}^{2}$

$155,000 \textrm{ cm}^{2}$

$15,050 \textrm{ cm}^{2}$

$150,500 \textrm{ cm}^{2}$

Correct answer:

$150,500 \textrm{ cm}^{2}$

Explanation:

Multiply each dimension by 100 to convert meters to centimeters:

$4.3 \times 100 = 430$

$3.5 \times 100 = 350$

Multiply these dimensions to get the area of the rectangle in square centimeters:

$430 \times 350 = 150,500\textrm{ cm}^{2}$

Report an Error

Example Question #2 : How To Find The Area Of A Trapezoid

Trapezoid

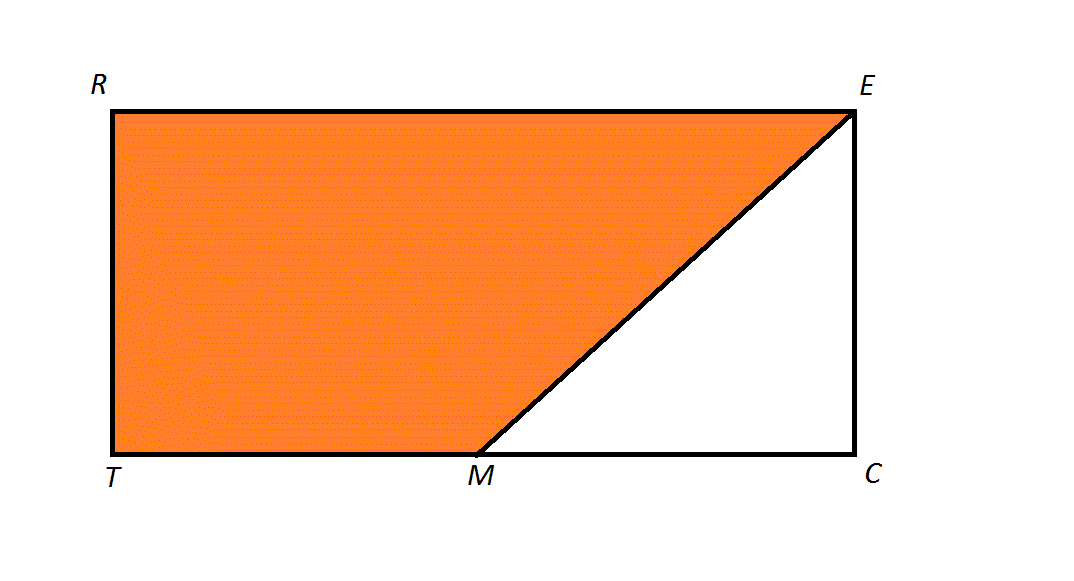
The above diagram depicts a rectangle RECT with isosceles triangle $\Delta ECM$ . If is the midpoint of $\overline{CT}$ , and the area of the orange region is , then what is the length of one leg of $\Delta ECM$ ?

Possible Answers:

$\sqrt {108}$

$\sqrt {54}$

$\sqrt {96}$

$\sqrt {48}$

Correct answer:

$\sqrt {48}$

Explanation:

The length of a leg of $\Delta ECM$ is equal to the height of the orange region, which is a trapezoid. Call this length/height .

Since the triangle is isosceles, then CM = h , and since is the midpoint of $\overline{CT}$ , MT = h . Also, since opposite sides of a rectangle are congruent,

RE = CT = CM + MT = h + h = 2h

Therefore, the orange region is a trapezoid with bases and and height . Its area is 72, so we can set up and solve this equation using the area formula for a trapezoid:

$\frac{1}{2} (B + b)h = 72$

$\frac{1}{2} (2h + h)h = 72$

$\frac{1}{2} (3h )h = 72$

$\frac{3}{2}h^{2} = 72$

$\frac{3}{2}h^{2} \cdot \frac{2}{3} = 72 \cdot \frac{2}{3}$

$h^{2}= 48$

$h = \sqrt {48}$

This is the length of one leg of the triangle.

Report an Error

Example Question #2 : How To Find The Area Of A Trapezoid

A trapezoid has a height of inches and bases measuring inches and inches. What is its area?

Possible Answers:

$900\; \textrm{in}^{2}$

$1,500\; \textrm{in}^{2}$

$864\; \textrm{in}^{2}$

$600\; \textrm{in}^{2}$

$750\; \textrm{in}^{2}$

Correct answer:

$750\; \textrm{in}^{2}$

Explanation:

Use the following formula, with B = 36,b = 24,h=25 :

$A = \frac{1}{2} (B+b)h = \frac{1}{2} (36+24) \cdot 25 = 750$

Report an Error

Example Question #51 : Geometry

What is the area of a triangle with a base of and a height of ?

Possible Answers:

Correct answer:

Explanation:

The formula for the area of a triangle is $\dpi{100} Area=\frac{1}{2}\times base\times height$ .

Plug the given values into the formula to solve:

$\dpi{100} Area=\frac{1}{2}\times 12\times 3$

$\dpi{100} Area=\frac{1}{2}\times 36$

$\dpi{100} Area=18$

Report an Error

Example Question #1231 : Concepts

Find the area of a square with side length 1.

Possible Answers:

Correct answer:

Explanation:

To solve, simply use the formula for the area of a square. Thus,

A=s^2=1^2=1

Report an Error

View Tutors

Kaitlyn
Certified Tutor

Fairfield University, Bachelor of Science, Biology, General. NUI Galway Ireland, Master of Science, Neuroscience.

View Tutors

Colton
Certified Tutor

Texas State University-San Marcos, Bachelor of Science, Mathematics.

View Tutors

Stephen
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor of Science, Geophysics and Seismology.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Los Angeles, Reading Tutors in San Diego, Math Tutors in Atlanta, Calculus Tutors in Chicago, Reading Tutors in New York City, Calculus Tutors in Houston, LSAT Tutors in San Diego, Statistics Tutors in San Francisco-Bay Area, Computer Science Tutors in Atlanta, ACT Tutors in Houston

Popular Courses & Classes

ISEE Courses & Classes in Philadelphia, LSAT Courses & Classes in Chicago, ACT Courses & Classes in Washington DC, Spanish Courses & Classes in Seattle, SSAT Courses & Classes in Seattle, GRE Courses & Classes in Miami, Spanish Courses & Classes in Los Angeles, SSAT Courses & Classes in Houston, LSAT Courses & Classes in San Diego, GRE Courses & Classes in Boston

Popular Test Prep

GRE Test Prep in Boston, LSAT Test Prep in Boston, SAT Test Prep in Phoenix, SAT Test Prep in Seattle, ISEE Test Prep in Phoenix, ISEE Test Prep in Houston, ACT Test Prep in Washington DC, LSAT Test Prep in San Diego, GRE Test Prep in San Diego, GMAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #1231 : Concepts

Example Question #1232 : Concepts

Example Question #41 : Geometry

Example Question #1231 : Concepts

Example Question #11 : Triangles

Example Question #161 : Geometry

Example Question #2 : How To Find The Area Of A Trapezoid

Example Question #2 : How To Find The Area Of A Trapezoid

Example Question #51 : Geometry

Example Question #1231 : Concepts

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: