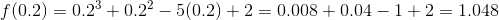All HiSET: Math Resources
Example Questions
Example Question #1 : Domain And Range Of A Function
Define functions 

Give the domain of the function 
The domain of the sum of two functions is the intersections of the domains of the individual functions. Both 

The domain of 

Adding 8 to both sides:
This domain is 
The domain of 

Subtracting 8 tfrom both sides:
This domain is
The domain of 

Example Question #1 : Domain And Range Of A Function
Define functions 
Give the domain of the composition 
None of the other choices gives the correct response.
None of the other choices gives the correct response.
The domain of the composition of functions 

















However, 




Example Question #3 : Domain And Range Of A Function
Define functions 

Give the domain of the function 
The domain of the difference of two functions is the intersections of the domains of the individual functions. Both 

The domain of 

Subtracting 8 tfrom both sides:
This domain is
The domain of 

Adding 

This domain is ![(-\infty , 8]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093604/gif.latex)
The domain of 
![[-8, 8]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093606/gif.latex)
Example Question #2 : Domain And Range Of A Function
Define functions ![f(x) = \sqrt[3]{x-8}](https://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093559/gif.latex)
![g(x) = \sqrt[3]{x+ 8}](https://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093560/gif.latex)
Give the domain of the function 
The domain of the sum of two functions is the intersections of the domains of the individual functions.
Both 




Example Question #1 : Domain And Range Of A Function
Define
Give the range of the function.
The range of a function is the set of all possible values of 
Since this function is piecewise-defined, it is necessary to examine both parts of the function and extract the range of each.
For 


or

For 


or
The overall range of 

Example Question #41 : Algebraic Concepts
A restaurant sets the prices of its dishes using the following function:
Price = (Cost of Ingredients) + (40% of the Cost of Ingredients) + 5
where all quantities are in U.S. Dollars.
If the cost of ingredients for a steak dish is $14, what will the restaurant set the price of the steak dish at?
$14
$24.60
$19.60
$19
$13.40
$24.60
The price of the dish is a function of a single variable, the cost of the ingredients. One way to conceptualize the problem is by thinking of it in function notation. Let 

"Price = (Cost of Ingredients) + (40% of the Cost of Ingredients) + 5"
into a regular equation with recognizable parts. Replace "Price" with 

Simplify by combining like terms (

The cost of ingredients for the steak dish is $14, so substitute 14 for 

All that's left is to compute the answer:
So, the steak dish will have a price of $24.60.
Example Question #2 : Functional Relationship Between Two Quantities

The plot shows the graphs of five different equations. Using shape and location, determine which graphed line corresponds to the equation 
Line E
Line C
Line B
Line A
Line D
Line B
The power of 

The equation is given in the slope-intercept form, 



In the given equation, the constant 
Example Question #271 : Hi Set: High School Equivalency Test: Math
The equation
has two distinct solutions. What is their sum?
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form 

If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient 


Example Question #44 : Algebraic Concepts
The graph of the polynomial function
has one and only one zero on the interval 
The Intermediate Value Theorem (IVT) states that if the graph of a function 
![[a, b]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex)












Example Question #1 : Use The Zeros To Construct A Rough Graph Of A Function
The graph of a function is shown below, with labels on the y-axis hidden.

Determine which of the following functions best fits the graph above.
Use the zeroes of the graph to determine the matching function. Zeroes are values of x where 
Visually, you can see that the curve crosses the x-axis when 


A function with a factor of 






The answer choice 



Certified Tutor
Certified Tutor
All HiSET: Math Resources


![[-8, 8]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093552/gif.latex)
![(-\infty , -8]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093554/gif.latex)
![(-\infty , 8]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093553/gif.latex)









![\left ( - \infty, 0 \right ]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1090649/gif.latex)




![[-8, 8]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093545/gif.latex)


![(-\infty , -8]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093548/gif.latex)
![(-\infty , 8]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093549/gif.latex)







![(-\infty, - 8]](https://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093557/gif.latex)
![(-\infty, 8]](https://cdn-s3.varsitytutors.com/uploads/formula_image/image/1093556/gif.latex)




![(-2, 3]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094856/gif.latex)

![(-\infty, -2] \cup (3, \infty)](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094854/gif.latex)