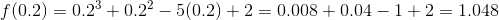We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

HiSET: Math : Zeroes of polynomials

Study concepts, example questions & explanations for HiSET: Math

Create An Account

All HiSET: Math Resources

125 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #43 : Algebraic Concepts

The equation

$x^{2} + 34 = 17x$

has two distinct solutions. What is their sum?

Possible Answers:

Correct answer:

Explanation:

It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.

First, get the equation in standard form $ax^{2}+ bx + c = 0$ by subtracting 17x from both sides:

$x^{2} + 34 = 17x$

$x^{2} + 34 -17x = 17x - 17x$

$x^{2} -17x + 34 = 0$

If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient . In this problem, b= -17 , making the correct choice.

Report an Error

Example Question #271 : Hi Set: High School Equivalency Test: Math

The graph of the polynomial function

$f(x)= x^{3}+x^{2}-5x+2$

has one and only one zero on the interval (0, 1) . On which subinterval is it located?

Possible Answers:

(0.8, 1)

(0.4, 0.6)

(0,6, 0.8)

(0.2, 0.4)

(0, 0.2)

Correct answer:

(0.4, 0.6)

Explanation:

The Intermediate Value Theorem (IVT) states that if the graph of a function is continuous on an interval [a, b] , and f(a) and f(b) differ in sign, then has a zero on (a,b) . Consequently, the way to answer this question is to determine the signs of on the endpoints of the subintervals - $\left \{ 0, 0.2, 0.4, 0.6, 0.8, 1 \right \}$ . We can do this by substituting each value for as follows:

$f(x)= x^{3}+x^{2}-5x+2$

$f(0)= 0^{3}+0^{2}-5(0)+2 = 0+0-0+2= 2$

$f(0.2)= 0.2^{3}+0.2^{2}-5(0.2)+2 = 0.008+0.04-1+2 = 1.048$

$f(0.4)= 0.4^{3}+0.4^{2}-5(0.4)+2= 0.064+ 0.16- 2+2 = 0.224$

$f(0.6)= 0.6^{3}+0.6^{2}-5(0.6)+2= 0.216+ 0.36- 3+2 = -0.424$

$f(0.8)= 0.8^{3}+0.8^{2}-5(0.8)+2= 0.512+ 0.64- 4+2 = -0.848$

$f(1)=1^{3}+1^{2}-5(1)+2 =1+1-5+2=-1$

assumes positive values for x= 0, 0.2, 0.4 and negative values for x = 0.6, 0.8, 1 . By the IVT, has a zero on (0.4, 0.6) .

Report an Error

Example Question #1 : Use The Zeros To Construct A Rough Graph Of A Function

The graph of a function is shown below, with labels on the y-axis hidden.

Graph zeroes 2

Determine which of the following functions best fits the graph above.

Possible Answers:

f(x)=-2x^2(x+1)(x-2)(x+2)

$f(x)=\frac{x+1}{x+2}$

f(x)=-2(x+1)(x-2)(x+2)

$f(x)=x^2x^{-2}$

f(x)=(x+1)^3(x-2)^2

Correct answer:

f(x)=-2(x+1)(x-2)(x+2)

Explanation:

Use the zeroes of the graph to determine the matching function. Zeroes are values of x where f(x)=0 . In other words, they are points on the graph where the curve touches zero.

Visually, you can see that the curve crosses the x-axis when x=-2 , x=-1 , and x=2 . Therefore, you need to look for a function that will equal zero at these x values.

A function with a factor of (x+2) will equal zero when x=-2 , because the factor of (x+2) will equal zero. The matching factors for the other two zeroes, x=-1 and x=2 , are (x+1) and (x-2) , respectively.

The answer choice f(x)=-2x^2(x+1)(x-2)(x+2) has all of these factors, but it is not the answer because it has an additional zero that would be visible on the graph. Notice it has a factor of x^2 , which results in a zero at x=0 . This additional zero that isn't present in the graph indicates that this cannot be matching function.

f(x)=-2(x+1)(x-2)(x+2) is the answer because it has all of the required factors and, as a result, the required zeroes, while not having additional zeroes. Notice that the constant coefficient of negative 2 does not affect where the zeroes are.

Report an Error

Example Question #1 : Use The Zeros To Construct A Rough Graph Of A Function

Graph zeroes

Which of the functions below best matches the graphed function?

Possible Answers:

f(x)= x(3x-5)(x+2)

f(x)= x(3x+5)(x-2)

f(x)= (3x+5)(x+2)

f(x)= x(3x-5)(x-2)

f(x)= x(x+2)^2

Correct answer:

f(x)= x(3x-5)(x+2)

Explanation:

First, look at the zeroes of the graph. Zeroes are where the function touches the x-axis (i.e. values of where f(x)=0 ).

The graph shows the function touching the x-axis when x=-2 , x=0 , and at a value in between 1.5 and 2.

Notice all of the possible answers are already factored. Therefore, look for one with a factor of (which will make f(x)=0 when x=0 ), a factor of (x+2) to make f(x)=0 when x=-2 , and a factor which will make f(x)=0 when is at a value between 1.5 and 2.

f(x)= x(3x-5)(x+2)

This function fills the criteria; it has an and an (x+2) factor. Additionally, the third factor, (3x-5) , will result in f(x)=0 when $x=\frac{5}{3}$ , which fits the image. It also does not have any extra zeroes that would contradict the graph.

Report an Error

View Tutors

Christy
Certified Tutor

York University, Bachelor in Arts, Psychology.

View Tutors

Shifrah
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Biology, General. Massachusetts College of Pharmacy and Health ...

View Tutors

Shakeel
Certified Tutor

All HiSET: Math Resources

125 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Los Angeles, MCAT Tutors in Washington DC, GRE Tutors in Phoenix, English Tutors in Seattle, SAT Tutors in San Diego, Statistics Tutors in Phoenix, SSAT Tutors in San Francisco-Bay Area, French Tutors in Philadelphia, Reading Tutors in Dallas Fort Worth, Biology Tutors in San Francisco-Bay Area

Popular Courses & Classes

SSAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Chicago, GRE Courses & Classes in Atlanta, SAT Courses & Classes in Washington DC, Spanish Courses & Classes in Washington DC, SAT Courses & Classes in Boston, ISEE Courses & Classes in Washington DC, Spanish Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Chicago, MCAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

SAT Test Prep in Washington DC, ISEE Test Prep in Houston, LSAT Test Prep in Chicago, GRE Test Prep in Atlanta, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Miami, LSAT Test Prep in Seattle, SSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Boston, GRE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HiSET: Math : Zeroes of polynomials

Study concepts, example questions & explanations for HiSET: Math

All HiSET: Math Resources

Example Questions

Example Question #43 : Algebraic Concepts

Example Question #271 : Hi Set: High School Equivalency Test: Math

Example Question #1 : Use The Zeros To Construct A Rough Graph Of A Function

Example Question #1 : Use The Zeros To Construct A Rough Graph Of A Function

All HiSET: Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: