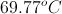We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Physics : Thermodynamics

Study concepts, example questions & explanations for High School Physics

Create An Account

All High School Physics Resources

6 Diagnostic Tests 233 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Understanding Heat And Temperature

0.75kg $\displaystyle 0.75kg$ of soup at $80^\circ C$ $\displaystyle 80^\circ C$ cools down to $20^\circ C$ $\displaystyle 20^\circ C$ after 2300s $\displaystyle 2300s$. If the specific heat of the soup is $\small 3.67\frac{kJ}{kg^\circ C}$ $\displaystyle \small 3.67\frac{kJ}{kg^\circ C}$, how much energy does the soup release into the room?

Possible Answers:

$\displaystyle 275.25kJ$

$\displaystyle 1651.5kJ$

0.72kJ $\displaystyle 0.72kJ$

27.53kJ $\displaystyle 27.53kJ$

$\displaystyle 165.15kJ$

Correct answer:

$\displaystyle 165.15kJ$

Explanation:

The formula for heat energy is:

$Q=mc\Delta t$ $\displaystyle Q=mc\Delta t$

We are given the initial and final temperatures, mass, and specific heat. Using these values, we can find the heat released. Note that the time is irrelevant to this calculation.

$Q=(0.75kg)(3.67\frac{kJ}{kg^\circ C})(20^\circ C -80^\circ C)$ $\displaystyle Q=(0.75kg)(3.67\frac{kJ}{kg^\circ C})(20^\circ C -80^\circ C)$

$\displaystyle Q=-165.15kJ$

That means that the soup "lost" $\displaystyle 165.15kJ$ of energy. This is the amount that it released into the room. The value is negative for the soup, the source of the heat, but positive for the room, which receives it.

Report an Error

Example Question #3 : Understanding Heat And Temperature

0.75kg $\displaystyle 0.75kg$ of soup cools down to $22^\circ C$ $\displaystyle 22^\circ C$after 2800s $\displaystyle 2800s$. If the specific heat of the soup is $\small 3.67\frac{kJ}{kg^\circ C}$ $\displaystyle \small 3.67\frac{kJ}{kg^\circ C}$, and it released 64.11kJ $\displaystyle 64.11kJ$of energy into the room, what was the initial temperature of the soup?

Possible Answers:

$45.29^\circ C$ $\displaystyle 45.29^\circ C$

$1.29^\circ C$ $\displaystyle 1.29^\circ C$

$0.03^\circ C$ $\displaystyle 0.03^\circ C$

$24.58^\circ C$ $\displaystyle 24.58^\circ C$

$-1.29^\circ C$ $\displaystyle -1.29^\circ C$

Correct answer:

$45.29^\circ C$ $\displaystyle 45.29^\circ C$

Explanation:

The formula for heat energy is:

$Q=mc\Delta t$ $\displaystyle Q=mc\Delta t$

We are given the final temperature, mass, specific heat, and heat released. Using these values, we can find the initial temperature. Note that the time is irrelevant to this calculation. Since heat is released from the soup, the net change in the soup's energy is negative. Since the soup is cooling, we expect our answer to be greater than $22^\circ C$ $\displaystyle 22^\circ C$.

$-64.11kJ=(0.75kg)(3.67\frac{kJ}{kg^\circ C})(22^\circ C- T_i)$ $\displaystyle -64.11kJ=(0.75kg)(3.67\frac{kJ}{kg^\circ C})(22^\circ C- T_i)$

$-64.11kJ=2.7525\frac{kJ}{^\circ C}*(22^\circ C - T_i)$ $\displaystyle -64.11kJ=2.7525\frac{kJ}{^\circ C}*(22^\circ C - T_i)$

$\frac{-64.11kJ}{2.7525\frac{kJ}{^\circ C}}=(22^\circ C -T_i )$ $\displaystyle \frac{-64.11kJ}{2.7525\frac{kJ}{^\circ C}}=(22^\circ C -T_i )$

$-23.29^\circ C=22^\circ C - T_i$ $\displaystyle -23.29^\circ C=22^\circ C - T_i$

$-45.29^\circ C=-T_i$ $\displaystyle -45.29^\circ C=-T_i$

$45.29^\circ C=T_i$ $\displaystyle 45.29^\circ C=T_i$

Report an Error

Example Question #2 : Understanding Heat And Temperature

0.75kg $\displaystyle 0.75kg$ of soup at $80^\circ C$ $\displaystyle 80^\circ C$ cools down after 2300s $\displaystyle 2300s$. If the specific heat of the soup is $\small 3.67\frac{kJ}{kg^\circ C}$ $\displaystyle \small 3.67\frac{kJ}{kg^\circ C}$, and it released 75.22kJ $\displaystyle 75.22kJ$ of energy into the room, what is the final temperature of the soup?

Possible Answers:

$0.023^\circ C$ $\displaystyle 0.023^\circ C$

$52.67^\circ C$ $\displaystyle 52.67^\circ C$

$107.33^\circ C$ $\displaystyle 107.33^\circ C$

$27.33^\circ C$ $\displaystyle 27.33^\circ C$

$43.67^\circ C$ $\displaystyle 43.67^\circ C$

Correct answer:

$52.67^\circ C$ $\displaystyle 52.67^\circ C$

Explanation:

The formula for heat energy is:

$Q=mc\Delta t$ $\displaystyle Q=mc\Delta t$

We are given the initial temperature, mass, specific heat, and heat released. Using these values, we can find the final temperature. Note that the time is irrelevant to this calculation. Since heat is released from the soup, the net change in the soup's energy is negative. Since the soup is cooling, we expect our answer to be less than $80^\circ C$ $\displaystyle 80^\circ C$.

$-75.22kJ=(0.75kg)(3.67\frac{kJ}{kg^\circ C})(T_f -80^\circ C)$ $\displaystyle -75.22kJ=(0.75kg)(3.67\frac{kJ}{kg^\circ C})(T_f -80^\circ C)$

$-75.22kJ=(2.7525\frac{kJ}{^\circ C})(T_f-80^\circ C)$ $\displaystyle -75.22kJ=(2.7525\frac{kJ}{^\circ C})(T_f-80^\circ C)$

$\frac{-75.22kJ}{2.7525\frac{kJ}{^\circ C}}=(T_f-80^\circ C)$ $\displaystyle \frac{-75.22kJ}{2.7525\frac{kJ}{^\circ C}}=(T_f-80^\circ C)$

$-27.33^\circ C=Tf-80^\circ C$ $\displaystyle -27.33^\circ C=Tf-80^\circ C$

$52.67^\circ C=T_f$ $\displaystyle 52.67^\circ C=T_f$

Report an Error

Example Question #21 : Thermodynamics

An ice cube at $0^\circ C$ $\displaystyle 0^\circ C$ melts. As it melts, constant temperature readings are taken and the sample maintains the temperature of $0^\circ$ $\displaystyle 0^\circ$ throughout the melting process. Which statement best describes the energy of the system?

Possible Answers:

Energy of the system remains the same

The form of water has no bearing on the system energy

Energy increases as the sample moves from a solid to a liquid

We would need to know the mass of the ice cube to draw a conclusion

Energy is being used to convert the ice to water

Correct answer:

Energy is being used to convert the ice to water

Explanation:

When an object changes phase, it requires energy called "latent heat." In this case, even though the temperature is remaining constant, the energy inside of the ice cube is decreasing as it expends energy to melt.

Report an Error

Example Question #3 : Understanding Heat And Temperature

A 280K $\displaystyle 280K$ silver spoon is placed in a 366K $\displaystyle 366K$ cup of tea. If the spoon has a mass of 32g $\displaystyle 32g$ and the tea has 90g $\displaystyle 90g$ of mass, what is the final temperature of the spoon?

$c_{tea}=1.00\frac{cal}{g*K}$ $\displaystyle c_{tea}=1.00\frac{cal}{g*K}$

$c_{silver}= 0.0558\frac{cal}{g*K}$ $\displaystyle c_{silver}= 0.0558\frac{cal}{g*K}$

Possible Answers:

353.43K $\displaystyle 353.43K$

288.32K $\displaystyle 288.32K$

323K $\displaystyle 323K$

364.33K $\displaystyle 364.33K$

301.21K $\displaystyle 301.21K$

Correct answer:

364.33K $\displaystyle 364.33K$

Explanation:

The equation for two items reaching a thermal equilibrium is given by describing a heat transfer. The heat removed from one object is equal to the heat added to the other.

$\displaystyle K_1=-K_2$

$K=mc\Delta T$ $\displaystyle K=mc\Delta T$

$m_1c_1\Delta T_1=-m_2c_2\Delta T_2$ $\displaystyle m_1c_1\Delta T_1=-m_2c_2\Delta T_2$

We are given the specific heat values of each substance, as well as their masses. We also know the initial temperature of each substance. Use these terms in the equation to solve for the final temperature. Remember that the final temperature will be the same for each substance, since they will be in thermodynamic equilibrium.

$(32g)(0.0558\frac{cal}{g*K})(T_f-280K)=-(90g)(1.00\frac{cal}{g*K})(T_f-366K)$ $\displaystyle (32g)(0.0558\frac{cal}{g*K})(T_f-280K)=-(90g)(1.00\frac{cal}{g*K})(T_f-366K)$

$1.7856\frac{cal}{K}*(T_f-280K)=-90\frac{cal}{g*K}*(T_f-366K)$ $\displaystyle 1.7856\frac{cal}{K}*(T_f-280K)=-90\frac{cal}{g*K}*(T_f-366K)$

$(1.7856\frac{cal}{K}*T_f)-499.968cal=(-90\frac{cal}{K}*T_f)+32940cal$ $\displaystyle (1.7856\frac{cal}{K}*T_f)-499.968cal=(-90\frac{cal}{K}*T_f)+32940cal$

$1.7856\frac{cal}{K}*T_f=(-90\frac{cal}{K}*T_f)+33439.968cal$ $\displaystyle 1.7856\frac{cal}{K}*T_f=(-90\frac{cal}{K}*T_f)+33439.968cal$

$91.7856\frac{cal}{K}*T_f=33439.968cal$ $\displaystyle 91.7856\frac{cal}{K}*T_f=33439.968cal$

$T_f=\frac{33439.968cal}{91.7856\frac{cal}{K}}$ $\displaystyle T_f=\frac{33439.968cal}{91.7856\frac{cal}{K}}$

$\displaystyle T_f=364.33K$

Report an Error

Example Question #7 : Understanding Heat And Temperature

A sample of 236g $\displaystyle 236g$ of water at $100^\circ C$ $\displaystyle 100^\circ C$ is placed in a 350g $\displaystyle 350g$ ceramic mug, which is at $23^\circ C$ $\displaystyle 23^\circ C$. What is the final temperature of the system?

$c_{ceramic}=1100\frac{J}{kg*^\circ C}$ $\displaystyle c_{ceramic}=1100\frac{J}{kg*^\circ C}$

$c_{water}=4.2\frac{J}{g*^\circ C}$ $\displaystyle c_{water}=4.2\frac{J}{g*^\circ C}$

Possible Answers:

$91^\circ C$ $\displaystyle 91^\circ C$

$123^\circ C$ $\displaystyle 123^\circ C$

$78.43^\circ C$ $\displaystyle 78.43^\circ C$

$108^\circ C$ $\displaystyle 108^\circ C$

$84^\circ C$ $\displaystyle 84^\circ C$

Correct answer:

$78.43^\circ C$ $\displaystyle 78.43^\circ C$

Explanation:

For this question, we must recognize that the system going to end up in equilibrium. That means that:

$m_1c_1\Delta T_1=-m_2c_2\Delta T_2$ $\displaystyle m_1c_1\Delta T_1=-m_2c_2\Delta T_2$

We are given the initial temperatures, masses, and specific heats of both the water and the ceramic. This will allow us to solve for the final temperature of the system; this value will be equal for both components. Notice that the specific heat given to us in the problem for the ceramic is in terms of kilograms, not grams. Convert to grams.

$(350g)(1.1\frac{J}{g*^\circ C})(T_f-23^\circ C)=-(236g)(4.2\frac{J}{g*^\circ C})(T_f-100^\circ C)$ $\displaystyle (350g)(1.1\frac{J}{g*^\circ C})(T_f-23^\circ C)=-(236g)(4.2\frac{J}{g*^\circ C})(T_f-100^\circ C)$

$(385\frac{J}{^\circ C})(T_f-23^\circ C)=-(991.2\frac{J}{^\circ C})(T_f-100^\circ C)$ $\displaystyle (385\frac{J}{^\circ C})(T_f-23^\circ C)=-(991.2\frac{J}{^\circ C})(T_f-100^\circ C)$

$\frac{(385\frac{J}{^\circ C})(T_f-23^\circ C)}{385\frac{J}{^\circ C}}=\frac{(-991.2\frac{J}{^\circ C})(T_f-100^\circ C)}{385\frac{J}{^\circ C}}$ $\displaystyle \frac{(385\frac{J}{^\circ C})(T_f-23^\circ C)}{385\frac{J}{^\circ C}}=\frac{(-991.2\frac{J}{^\circ C})(T_f-100^\circ C)}{385\frac{J}{^\circ C}}$

$T_f-23^\circ C=(-2.57)(T_f-100^\circ C)$ $\displaystyle T_f-23^\circ C=(-2.57)(T_f-100^\circ C)$

$T_f-23^\circ C=-2.57T_f+257^\circ C$ $\displaystyle T_f-23^\circ C=-2.57T_f+257^\circ C$

$-23^\circ C=-3.57T_f+257^\circ C$ $\displaystyle -23^\circ C=-3.57T_f+257^\circ C$

$-280^\circ C=-3.57T_f$ $\displaystyle -280^\circ C=-3.57T_f$

$\frac{-3.57T_f}{-3.57}=\frac{-280^\circ C}{-3.57}$ $\displaystyle \frac{-3.57T_f}{-3.57}=\frac{-280^\circ C}{-3.57}$

$T_f=78.43^\circ C$ $\displaystyle T_f=78.43^\circ C$

Report an Error

Example Question #8 : Understanding Heat And Temperature

A 78g $\displaystyle 78g$ vial of an unknown liquid is $9 8^\circ C$ $\displaystyle 9 8^\circ C$. Julie adds $\displaystyle 3g$ of the same liquid at $40^\circ C$ $\displaystyle 40^\circ C$ to the vial. What is the final temperature?

Possible Answers:

We need to know the freezing/boiling points of the liquid in order to solve.

$95.85^\circ C$ $\displaystyle 95.85^\circ C$

$94.74^\circ C$ $\displaystyle 94.74^\circ C$

We need to know the specific heat of the liquid in order to solve.

$7 7 . 6 4 ^\circ C$ $\displaystyle 7 7 . 6 4 ^\circ C$

Correct answer:

$95.85^\circ C$ $\displaystyle 95.85^\circ C$

Explanation:

The equation for change in temperature is $m_1c_1\Delta T_1=-m_2c_2\Delta T_2$ $\displaystyle m_1c_1\Delta T_1=-m_2c_2\Delta T_2$

Plug in our given values.

$m_1c_1\Delta T_1=-m_2c_2\Delta T_2$ $\displaystyle m_1c_1\Delta T_1=-m_2c_2\Delta T_2$

$0.78kg*c*(T_f-98^\circ C)=-0.03kg*c*(T_f -40^\circ C)$ $\displaystyle 0.78kg*c*(T_f-98^\circ C)=-0.03kg*c*(T_f -40^\circ C)$

Notice that the specific heats will cancel out.

$0.78kg*(T_f-98^\circ C)=-0.03kg*(T_f -40^\circ C)$ $\displaystyle 0.78kg*(T_f-98^\circ C)=-0.03kg*(T_f -40^\circ C)$

$(0.78kg*T_f)-(0.78kg*98^\circ C)=(-0.03kg*T_f)+(0.03kg*40^\circ C)$ $\displaystyle (0.78kg*T_f)-(0.78kg*98^\circ C)=(-0.03kg*T_f)+(0.03kg*40^\circ C)$

$(0.78kg*T_f)-(76.44kg*^\circ C)=(-0.03kg*T_f)+(1.2kg*^\circ C)$ $\displaystyle (0.78kg*T_f)-(76.44kg*^\circ C)=(-0.03kg*T_f)+(1.2kg*^\circ C)$

Combine like terms.

$(0.78kg*T_f)-(-0.03kg*T_f)=(1.2kg*^\circ C)+(76.44kg*^\circ C)$ $\displaystyle (0.78kg*T_f)-(-0.03kg*T_f)=(1.2kg*^\circ C)+(76.44kg*^\circ C)$ $0.81kg*T_f=77.64kg*^\circ C$ $\displaystyle 0.81kg*T_f=77.64kg*^\circ C$

$T_f=\frac{77.64kg*^\circ C}{0.81kg}{}$ $\displaystyle T_f=\frac{77.64kg*^\circ C}{0.81kg}{}$

$T_f=95.85^\circ C$ $\displaystyle T_f=95.85^\circ C$

Report an Error

Example Question #21 : Thermodynamics

A $\displaystyle 2g$ disc of copper is dropped into a 12g $\displaystyle 12g$ glass of water. If the copper was at $85^\circ C$ $\displaystyle 85^\circ C$ and the water was at $70^\circ C$ $\displaystyle 70^\circ C$, what is the new temperature of the mixture?

$c_{Cu}=0.092\frac{cal}{g^oC}$ $\displaystyle c_{Cu}=0.092\frac{cal}{g^oC}$

$c_{water}=1.00\frac{cal}{g^oC}$ $\displaystyle c_{water}=1.00\frac{cal}{g^oC}$

Possible Answers:

$\displaystyle 69.77^oC$

$\displaystyle 70.23^oC$

$\displaystyle 79.77^oC$

$\displaystyle 83.76^oC$

$\displaystyle 75.22^oC$

Correct answer:

$\displaystyle 70.23^oC$

Explanation:

The relationship between mass and temperature, when two masses are mixed together, is:

$m_1c_1\Delta T=-m_2c_2\Delta T$ $\displaystyle m_1c_1\Delta T=-m_2c_2\Delta T$

Using the given values for the mass and specific heat of each compound, we can solve for the final temperature.

$(2g)(0.092\frac{cal}{g*^\circ C})(T_f-85^\circ C)=-(12g)(1\frac{cal}{g*^\circ C})(T_f-70^{\circ} C)$ $\displaystyle (2g)(0.092\frac{cal}{g*^\circ C})(T_f-85^\circ C)=-(12g)(1\frac{cal}{g*^\circ C})(T_f-70^{\circ} C)$

We need to work to isolate the final temperature.

$(0.184\frac{cal}{^\circ C})(T_f-85^\circ C)=-(12\frac{cal}{^\circ C})(T_f-70^{\circ} C)$ $\displaystyle (0.184\frac{cal}{^\circ C})(T_f-85^\circ C)=-(12\frac{cal}{^\circ C})(T_f-70^{\circ} C)$

Distribute into the parenthesis using multiplication.

$(0.184\frac{cal}{^\circ C})T_f-15.64cal=(-12\frac{cal}{^\circ C})T_f+840cal$ $\displaystyle (0.184\frac{cal}{^\circ C})T_f-15.64cal=(-12\frac{cal}{^\circ C})T_f+840cal$

Combine like terms.

$(12.184\frac{cal}{^oC})T_f=855.64cal\textup{}$ $\displaystyle (12.184\frac{cal}{^oC})T_f=855.64cal\textup{}$

$T_f=\frac{855.64cal}{12.184\frac{cal}{^oC}}$ $\displaystyle T_f=\frac{855.64cal}{12.184\frac{cal}{^oC}}$

$T_f=70.23^\circ C$ $\displaystyle T_f=70.23^\circ C$

Report an Error

Example Question #1 : Understanding Effects Of Heat On Volume

An ideal gas is inside of a container with a pressure of 2Pa $\displaystyle 2Pa$. If it starts with a volume of $\displaystyle 1L$ and is compressed to 0.5L $\displaystyle 0.5L$, what is the new pressure if the temperature remains constant?

Possible Answers:

10Pa $\displaystyle 10Pa$

2Pa $\displaystyle 2Pa$

8Pa $\displaystyle 8Pa$

0.5Pa $\displaystyle 0.5Pa$

4Pa $\displaystyle 4Pa$

Correct answer:

4Pa $\displaystyle 4Pa$

Explanation:

We will need to use Boyle's Law to solve:

$\displaystyle P_1V_1=P_2V_2$

Boyle's Law allows us to set up a relationship between the changes in pressure and volume under conditions with constant temperature. Since the equation is a proportion, we do not need to convert any units.

We can use the given values to solve for the new pressure.

$\displaystyle (2Pa)(1L)=(P_2)(0.5L)$

$\frac{(2Pa)(1L)}{0.5L}=(P_2)$ $\displaystyle \frac{(2Pa)(1L)}{0.5L}=(P_2)$

$\frac{2Pa\cdot L}{0.5L}=P_2$ $\displaystyle \frac{2Pa\cdot L}{0.5L}=P_2$

4Pa=P_2 $\displaystyle 4Pa=P_2$

Report an Error

Example Question #611 : High School Physics

An ideal gas is inside of a tube at 60^oC $\displaystyle 60^oC$. If the pressure remains constant, but the volume decreases from 5m^3 $\displaystyle 5m^3$ to 3m^3 $\displaystyle 3m^3$, what will be the final temperature in the tube?

Possible Answers:

18^oC $\displaystyle 18^oC$

36^oC $\displaystyle 36^oC$

120^oC $\displaystyle 120^oC$

180^oC $\displaystyle 180^oC$

24^oC $\displaystyle 24^oC$

Correct answer:

36^oC $\displaystyle 36^oC$

Explanation:

For this problem, use Charles's Law:

$\frac{V_1}{T_1}=\frac{V_2}{T_2}$ $\displaystyle \frac{V_1}{T_1}=\frac{V_2}{T_2}$

In this formula, $\displaystyle V$ is the volume and $\displaystyle T$ is the temperature. Charles's Law allows us to set up a proportion for changes in volume and temperature, as long as pressure remains constant. Since we are dealing with a proportion, the units for temperature are irrelevant and we do not need to convert to Kelvin.

Using the given values, we should be able to solve for the final temperature.

$\frac{V_1}{T_1}=\frac{V_2}{T_2}$ $\displaystyle \frac{V_1}{T_1}=\frac{V_2}{T_2}$

$\frac{5m^3}{60^oC}=\frac{3m^3}{T_2}$ $\displaystyle \frac{5m^3}{60^oC}=\frac{3m^3}{T_2}$

Cross multiply.

$\displaystyle 5m^3* T_2=3m^3* 60^oC$

$5m^3* T_2=180(^oC\cdot m^3)$ $\displaystyle 5m^3* T_2=180(^oC\cdot m^3)$

$T_2=\frac{180(^{\circ}C\cdot m^3)}{5m^3}$ $\displaystyle T_2=\frac{180(^{\circ}C\cdot m^3)}{5m^3}$

$T_2=36^{\circ}C$ $\displaystyle T_2=36^{\circ}C$

Report an Error

View Tutors

Katie
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor of Science, Economics.

View Tutors

Chhavi
Certified Tutor

SUNY at Binghamton, Master of Science, Mathematics.

View Tutors

Tierney
Certified Tutor

Williams College, Bachelor of Science, English.

All High School Physics Resources

6 Diagnostic Tests 233 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Phoenix, Statistics Tutors in New York City, Statistics Tutors in Denver, GMAT Tutors in Washington DC, ISEE Tutors in Atlanta, ACT Tutors in Seattle, Calculus Tutors in San Diego, Statistics Tutors in San Francisco-Bay Area, Calculus Tutors in Philadelphia, SAT Tutors in Denver

Popular Courses & Classes

GMAT Courses & Classes in Atlanta, MCAT Courses & Classes in Seattle, MCAT Courses & Classes in Denver, ISEE Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Boston, SAT Courses & Classes in Chicago, SSAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Houston, LSAT Courses & Classes in Denver, LSAT Courses & Classes in Washington DC

Popular Test Prep

SSAT Test Prep in Washington DC, LSAT Test Prep in Miami, SAT Test Prep in Boston, SSAT Test Prep in San Diego, MCAT Test Prep in New York City, MCAT Test Prep in Dallas Fort Worth, SAT Test Prep in Chicago, GMAT Test Prep in Houston, SAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Physics : Thermodynamics

Study concepts, example questions & explanations for High School Physics

All High School Physics Resources

Example Questions

Example Question #1 : Understanding Heat And Temperature

Example Question #3 : Understanding Heat And Temperature

Example Question #2 : Understanding Heat And Temperature

Example Question #21 : Thermodynamics

Example Question #3 : Understanding Heat And Temperature

Example Question #7 : Understanding Heat And Temperature

Example Question #8 : Understanding Heat And Temperature

Example Question #21 : Thermodynamics

Example Question #1 : Understanding Effects Of Heat On Volume

Example Question #611 : High School Physics

All High School Physics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: