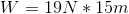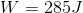We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Physics : Energy and Work

Study concepts, example questions & explanations for High School Physics

Create An Account

All High School Physics Resources

6 Diagnostic Tests 233 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Calculating Work

A cat knocks a 0.01kg toy mouse across the floor with of force. If the toy travels , how much work did the cat do?

Possible Answers:

$\frac{1}{2}J$

16J

Correct answer:

Explanation:

The relationship between work, force and distance is:

W=F*d

We are given the value for the force and the distance that the toy travels. Using these values, we can find the work done by the cat. Note that the mass of the toy is not relevant for this calculation.

W=2N*4m

W=8J

Report an Error

Example Question #2 : Calculating Work

A cat knocks a 0.01kg toy mouse across the floor. If it travels and the cat does of work, how much force did the cat exert on the mouse?

Possible Answers:

$\frac{5}{7}N$

$\frac{7}{5}N$

12N

35N

Correct answer:

$\frac{7}{5}N$

Explanation:

The relationship between work, force and distance is:

W=F*d

We are given the value for the work done by the cat and the distance that the toy travels. Using these values, we can find the force on the toy. Note that the mass of the toy is not relevant for this calculation.

7J=F*5m

$\frac{7J}{5m}=F$

$\frac{7}{5}N=F$

Report an Error

Example Question #12 : Mechanics

A 30kg crate is pushed 15m across the floor. If 19N of force was used to achieve this motion, how much work was done?

Possible Answers:

1.3J

30J

285J

5586J

Correct answer:

285J

Explanation:

The formula for work is:

W=F*d

Given the values for force and distance, we can calculate the work done.

W=19N*15m

W=285J

Note that no work is done by the force of gravity or the weight of the box, since the vertical position does not change.

Report an Error

Example Question #4 : Calculating Work

Ryan pushes a 14kg filing cabinet 2.1m across the floor, doing 88.2J of work. How much force is he applying to the cabinet?

Possible Answers:

42N

137.2N

13.23N

9.8N

Correct answer:

42N

Explanation:

Work is the product of force times a distance:

W=F*d

We are given the work and the distance traveled, allowing us to solve for the force. The mass of the cabinet is not necessary information.

W=F*d

88.2J=F(2.1m)

$\frac{88.2J}{2.1m}=F$

42N=F

Report an Error

Example Question #10 : Calculating Work

A 1500kg rocket has a net propulsion force of 500N. Over a short period of time, the rocket speeds up uniformly from an initial velocity of $40\frac{m}{s}$ to a final velocity of $50\frac{m}{s}$ . Assume that the mass of the rocket remains constant even though it is burning fuel and that the net force is along the direction of travel. What is the net work done on the rocket in kJ?

Possible Answers:

None of these

475kJ

575kJ

375kJ

675 kJ

Correct answer:

675 kJ

Explanation:

Use the data given to calculate the kinetic energy of the rocket at the two different velocities. Then find the amount of work done using the following equation:

$W=\Delta KE$

Kinetic energy of the rocket at the two velocities:

$KE=\frac{1}{2}mv^2=.5(1500kg)(50)^2=1875000J$

$KE=\frac{1}{2}mv^2=.5(1500kg)(40)^2=1200000J$

The change in the kinetic energy at the two velocities:

$W=\Delta KE=1875000-1200000=675000J$

W=675kJ

Report an Error

Example Question #1 : Work Kinetic Energy Theorem

What is the work applied to a 1000kg car when it is pushed 1000m up along a 10 degree incline at a constant velocity.. Assume the coefficient of friction between the car and the ramp is 0.30 .

Possible Answers:

6.1x10^6J

4.6x10^6J

5.7x10^6J

1.9x10^6J

2.3x10^6J

Correct answer:

4.6x10^6J

Explanation:

Known

m = 1000kg

$\Delta x= 1000m$

$\Theta = 100$

$\mu = 0.30$

Unknown

W = ?

The work done on the object is equal to the net force done on the object multiplied by the displacement through which the force acts.

W = Fd

Therefore the first thing to do in this problem is to determine the amount of force needed to push the car up the incline. Since the car is moving at a constant velocity, all forces must be balanced. The force in the direction of motion is the force applied which is doing work on the object. The forces opposing motion are the force of friction and the x-component of the gravitational force.

To determine the Force of Gravity in the x-direction, we must break the force of gravity into components and examine the side acting in the x-direction. Using trigonometric functions we get that

$F_{GXdirection} = F_Gsin(\Theta )$

We know that the force of gravity is equal to mg

$F_{GXdirection} = mgsin(\Theta )$

The force of friction is directly related to μ (the coefficient of friction) times the normal force. In this case the normal force is equal to the y component of the force of gravity.

$F_{GYdirection} = mgcos(\Theta )$

Therefore

$F_{friction}=\mu *F_N$

$F_N=F_{GYdirection}$

$F_{friction}=\mu *mgcos(\Theta )$

We know that our force applied must balance both of these forces.

$F_{applied} = mgsin(\Theta )+\mu *mgcos(\Theta )$

We can now substitute this equation into our work each to determine the work applied to the car.

$W = (mgsin(\Theta )+\mu *mgcos(\Theta ))d$

We can now substitute in our variables and solve for the missing piece.

$W = ((1000kg)(9.8m/s^2)(sin(10\degree) + (0.3)(1000kg)(9.8m/s^2)(cos(10\degree))(1000m)$

W = 4.6x10^6J

Report an Error

Example Question #2 : Work Kinetic Energy Theorem

At an accident science on a level road, investigators measure a car’s skid mark to be 90m long. The accident occurred on a rainy day, the coefficient of friction was estimated to be 0.35 . What was the speed of the car when the driver slammed on and locked the brakes?

Possible Answers:

24.8m/s

48.4m/s

26.3m/s

36.4m/s

Correct answer:

24.8m/s

Explanation:

Knowns

d = 90m

$\mu = 0.35$

Unknown

v = ?

We know that the force of friction is what caused the skid marks and is the cause of the work done on car to slow it to a stop. We also know that the work is equal to the change in kinetic energy.

$-W = \Delta KE$

$-W = \frac{1}{2}mv_f^2 -\frac{1}{2} mv_i^2$

Work is equal to the force times the displacement over which the force acted.

-W = Fd

Therefore

$-Fd = \frac{1}{2} mv_f^2 -\frac{1}{2} mv_i^2$

The force in this case is the force of friction.

$F_{friction}=\mu *F_N$

Since the car is on a level road the normal force is equal and opposite the force of gravity.

F_N=F_G

The force of gravity is equal to the mass times the acceleration due to gravity

F_G = mg

Therefore

$F_{friction}=\mu mg$

We can substitute this in for our work-kinetic energy equation.

$-\mu mgd= \frac{1}{2} mv_f^2 -\frac{1}{2} mv_i^2$

Since the final velocity is we can cancel this out of the problem.

$-\mu mgd= -\frac{1}{2} mv_i^2$

Since there is a negative and a mass in both terms we can cancel these out of the equation

$\mu gd= \frac{1}{2} v_i^2$

Now we can substitute in our values and solve.

$(0.35)(9.8m/s^2)(90m) = \frac{1}{2} v_i^2$

v_i^2 = 617.4

v_i = 24.8m/s

Report an Error

Example Question #1 : Work Kinetic Energy Theorem

A cat knocks a 0.01kg toy mouse across the floor with of force. If the cat did 12J of work, how far did the mouse travel?

Possible Answers:

36m

12m

48m

Correct answer:

Explanation:

The relationship between work, force, and distance is:

W=F*d

We are given the force on the toy and the work done. Using these values, we can find the distance. Note that the mass is not relevant for this question.

12J=3N*d

12J3N=d

4m=d

Report an Error

Example Question #1 : Work Kinetic Energy Theorem

A 1500kg rocket has a net propulsion force of 500N . Over a short period of time, the rocket speeds up uniformly from an initial velocity of 40ms to a final velocity of 50ms . Assume that the mass of the rocket remains constant even though it is burning fuel and that the net force is along the direction of travel. What is the net work done on the rocket in ?

Possible Answers:

None of these

575kJ

675kJ

375kJ

475kJ

Correct answer:

675kJ

Explanation:

Use the data given to calculate the kinetic energy of the rocket at the two different velocities. Then find the amount of work done using the following equation:

$W=\Delta KE$

Kinetic energy of the rocket at the two velocities:

$KE= \frac{1}{2} mv^2 = .5 (1500kg)(50)^2 = 1875000J$

$KE = \frac{1}{2}mv^2 = .5(1500kg)(40)^2 = 1200000J$

The change in the kinetic energy at the two velocities:

$W=\Delta KE=1875000-1200000=675000J$

W=675kJ

Report an Error

Example Question #1 : Work Kinetic Energy Theorem

A bodybuilder lifts a 20kg weight upward 0.5m , and then returns it to its original position, all with a constant speed. What is the net work done on the weight?

Possible Answers:

10J

98J

196J

40J

Correct answer:

Explanation:

Work is a vector quantity equal to the change in energy in a given direction. Our net work will be equal to product of force and displacement.

$W_{net}=Fd$

We can write this equation in terms of Newton's second law to incorporate our given values.

$W_{net}=mgd=(20kg)(-9.8m/s^2)d$

During its motion the weight travels a distance of 0.5m upward, and then 0.5m downward. Its total distance will be 1.0m, however, we are looking for its displacement. The initial height and final height are equal, making the displacement equal to zero.

$W_{net}=(20kg)(-9.8m/s^2)(0m)$

$W_{net}=0J$

The total work will be zero because there was no net displacement.

Report an Error

View Tutors

Paarth
Certified Tutor

New Jersey Institute of Technology, Bachelor of Science, Computer Science.

View Tutors

Joshua
Certified Tutor

Murray State University, Bachelor in Arts, Spanish. Lipscomb University, Bachelor of Science, Teacher Assistant.

View Tutors

Kaylee
Certified Tutor

Brigham Young University, Bachelor, MFA - Animation.

All High School Physics Resources

6 Diagnostic Tests 233 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Los Angeles, English Tutors in Dallas Fort Worth, English Tutors in Philadelphia, Calculus Tutors in Seattle, Reading Tutors in San Diego, Algebra Tutors in Miami, GMAT Tutors in Denver, Math Tutors in Dallas Fort Worth, SSAT Tutors in Washington DC, Biology Tutors in Los Angeles

Popular Courses & Classes

ACT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Washington DC, SAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Los Angeles, MCAT Courses & Classes in Washington DC, SAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Los Angeles, LSAT Courses & Classes in Phoenix, ACT Courses & Classes in Chicago, SSAT Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in Atlanta, SSAT Test Prep in New York City, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Boston, SSAT Test Prep in Denver, MCAT Test Prep in Dallas Fort Worth, ACT Test Prep in Phoenix, ACT Test Prep in San Diego, SSAT Test Prep in Philadelphia, GMAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Physics : Energy and Work

Study concepts, example questions & explanations for High School Physics

All High School Physics Resources

Example Questions

Example Question #1 : Calculating Work

Example Question #2 : Calculating Work

Example Question #12 : Mechanics

Example Question #4 : Calculating Work

Example Question #10 : Calculating Work

Example Question #1 : Work Kinetic Energy Theorem

Example Question #2 : Work Kinetic Energy Theorem

Example Question #1 : Work Kinetic Energy Theorem

Example Question #1 : Work Kinetic Energy Theorem

Example Question #1 : Work Kinetic Energy Theorem

All High School Physics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: