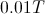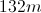All High School Physics Resources
Example Questions
Example Question #1 : Magnetism And Electromagnetism
A current of 

Ampere's law states:

In other words, the magnetic field (


We are given the current, the constant, and the radius. Using these values, we can solve for the magnetic field strength.
Notice that the 
Example Question #1 : Understanding The Right Hand Rules
A current runs through a wire such that it generates a magnetic field. The magnetic field is in the clockwise direction in the plane of your computer screen. What is the direction of the current?
Out of the screen
More information is needed to solve
Into the screen
Clockwise
Counter-clockwise
Into the screen
To solve this problem use the right hand rule. Take your right hand and make a fist. Now stick your thumb straight up. This will show you the relationship between current and magnetic field: if the magnetic field is your fingers, the current is your thumb.
In this problem, the only way you can get your fingers to be going clockwise in a plane is if your thumb is pointed directly at that plane. Point your thumb directly at the screen. Your fingers will naturally curl in the clockwise direction. The current must be going into the screen.
Example Question #2 : Understanding The Right Hand Rules
A current runs through a straight wire from right to left. What direction would the magnetic field be?
Into the screen
Out of the screen
Right to left
Left to right
Counter-clockwise
Counter-clockwise
For this problem, use the right hand rule. Take your right hand, stick your thumb straight up and curl your fingers around in a "thumbs up" shape.
If your thumb is the current, your fingers will be the magnetic field. With your thumb pointing to the left (the direction of the current), your fingers will curl in a counter-clockwise direction.
Note that the right hand rule for a straight wire is different from the right hand rule for a planar magnetic field!
Example Question #1 : Understanding The Right Hand Rules
A straight wire carries a current directly into your computer screen. In what direction would the magnetic field be?
Counter-clockwise
Into the screen
Right to left
Out of the screen
Clockwise
Clockwise
For this problem, use the right hand rule. Take your right hand, stick your thumb straight up, and curl your fingers around in a "thumbs up" shape.
If your thumb is the current, your fingers will be the magnetic field. With your thumb pointing away from your face, or toward your computer screen (the direction of the current), your fingers will curl in a clockwise direction.
Note that the right hand rule for a straight wire is different from the right hand rule for a planar magnetic field!
Example Question #61 : Electricity And Magnetism
A straight wire carries a current directly out of your computer screen. In what direction would the magnetic field be?
Clockwise
Counter-clockwise
Into the screen
Left to right
Out of the screen
Counter-clockwise
For this problem, use the right hand rule. Take your right hand, stick your thumb straight up, and curl your fingers around in a "thumbs up" shape.
If your thumb is the current, your fingers will be the magnetic field. With your thumb pointing toward your face, or out from your computer screen (the direction of the current), your fingers will curl in a counter-clockwise direction.
Note that the right hand rule for a straight wire is different from the right hand rule for a planar magnetic field!
Example Question #2 : Understanding The Right Hand Rules
A negatively charged particle is moving to the right along a vertical plane. If the force generated by a constant magnetic field is directed upwards within plane, in what direction is the magnetic field?
Out of the plane, away from the observer
Out of the plane, toward the observer
Downwards within the plane
Upward within the plane
Out of the plane, toward the observer
This question requires you to apply the right hand rule. Your thumb will point to the right, in the direction of the particle's velocity. For the negatively charged particle to feel an upward force, the back of your hand, not your palm as would be the case with a positively charged particle needs to be facing up. Extension of your fingers makes the magnetic field point out of the plane, toward you.
Example Question #1 : Understanding Magnetic Fields
A current of 

Ampere's law states:

In other words, the magnetic field (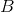
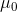

We are given the current, the constant, and the magnetic field strength. Using these values, we can solve for the magnetic field radius.
Notice that the 
All High School Physics Resources