All High School Math Resources
Example Questions
Example Question #2 : Law Of Sines
In 




Since we are given 


Substitute in the above equation:
Cross-multiply and solve for 
Example Question #3 : Law Of Sines
In 




No triangle can exist with these characteristics.
Since we are given 




Substitute and solve for 
Take the inverse sine of 0.6355:
There are two angles between 


This, however, is impossible, since this would result in the sum of the triangle measures being greater than 

Example Question #92 : Trigonometry

In this figure, angle 



Undefined
For this problem, use the law of sines:
%7D)
In this case, we have values that we can plug in:
Example Question #11 : Triangles
 In this figure, if angle
In this figure, if angle 



(NOTE: Figure not necessarily drawn to scale.)
Undefined
First, observe that this figure is clearly not drawn to scale. Now, we can solve using the law of sines:

In this case, we have values that we can plug in:
Example Question #1 : Finding Sides
There is not enough information
The side-angle-side (SAS) postulate can be used to determine that the triangles are similar. Both triangles share the angle farthest to the right. In the smaller triangle, the upper edge has a length of 



The statement is true, so the triangles must be similar.
We can use this ratio to solve for the missing side length.
To simplify, we will only use the lower edge and left edge comparison.
Cross multiply.
Example Question #11 : Triangles
We can solve using the trigonometric definition of tangent.
We are given the angle and the adjacent side.
We can find 
Example Question #12 : Triangles

If 




Not enough information to solve
This problem can be easily solved using trig identities. We are given the hypotenuse 



Rearrange to solve for 
If you calculated the side to equal 


Example Question #2 : Graphing The Sine And Cosine Functions

What is the length of CB?
All High School Math Resources










































 .
.


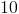






 .
.





























