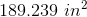Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Non-Cubic Prisms

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Prisms

The length of a box is 3 times the width. Which of the following gives the length (L inches) in terms of the width (W inches) of the box?

Possible Answers:

L = 3W

L = 3/W

L = ½ (3W)

L = W + 3

Correct answer:

L = 3W

Explanation:

When reading word problems, there are certain clues that help interpret what is going on. The word “is” generally means “=” and the word “times” means it will be multiplied by something. Therefore, “the length of a box is 3 times the width” gives you the answer: L = 3 x W, or L = 3W.

Report an Error

Example Question #82 : Solid Geometry

The width of a box, in inches, is 5 inches less than three times its length. Which of the following equations gives the width, W inches, in terms of the length, L inches, of the box?

Possible Answers:

W=3-5L

W=5-3L

W=3L-5

W=5L-3

Correct answer:

W=3L-5

Explanation:

We notice the width is “5 inches less than three times its width,” so we express W as being three times its width (3L) and 5 inches less than that is 3L minus 5. In this case, W is the dependent and L is the independent variable.

W = 3L - 5

Report an Error

Example Question #2 : Non Cubic Prisms

Angie is painting a 2 foot cube for a play she is in. She needs $25\hspace{1 mm}mL$ of paint for every square foot she paints. How much paint does she need?

Possible Answers:

$600\hspace{1 mm}mL$

$1.041\overline{6}\hspace{1 mm}mL$

$100\hspace{1 mm}mL$

None of the available answers

It is impossible to convert between metric units and feet.

Correct answer:

$600\hspace{1 mm}mL$

Explanation:

First we must calculate the surface area of the cube. We know that there are six surfaces and each surface has the same area:

$Area=6(2^2)=6\times 4=24\hspace{1 mm}feet^2$

Now we will determine the amount of paint needed

$24\hspace{1 mm}feet^2\times \frac{25\hspace{1 mm}mL}{1\hspace{1 mm}foot^2}=600\hspace{1 mm}mL$

Report an Error

Example Question #3 : Non Cubic Prisms

Find the surface area of the following triangular prism.

Half_box

Possible Answers:

$144 + 52\sqrt{2} m^2$

$54 + 144\sqrt{3} m^2$

$54 + 144\sqrt{2} m^2$

$144 + 54\sqrt{3} m^2$

$144 + 54\sqrt{2} m^2$

Correct answer:

$144 + 54\sqrt{2} m^2$

Explanation:

The formula for the surface area of a triangular prism is:

$SA = 2 (base) + lateral\ area$

$SA = 2 \cdot \left(\frac{1}{2}\right)(l)(w) + (l+w+y)(h)$

Where is the length of the triangle, is the width of the triangle, is the hypotenuse of the triangle, and is the height of the prism

Use the formula for a 45-45-90 triangle to solve for the length of the hypotenuse:

$s-s-s\sqrt{2}$

$6-6-6\sqrt{2}$

Plugging in our values, we get:

$SA = (6m)(6m) + (6m+6m+6\sqrt{2}m)(9m)$

$SA = (6m)(6m) + (12m + 6\sqrt{2}m)(9m)$

$SA = 36m^2 + 108m^2 + 54\sqrt{2}m^2 = 144 + 54\sqrt{2} m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Prism

Find the surface area of the following triangular prism.

Half_box

Possible Answers:

$256m^2 + 96\sqrt{2}m^2$

$96m^2 + 96\sqrt{2}m^2$

$256m^2 + 94\sqrt{2}m^2$

$256m^2 + 256\sqrt{2}m^2$

$96m^2 + 256\sqrt{2}m^2$

Correct answer:

$256m^2 + 96\sqrt{2}m^2$

Explanation:

The formula for the surface area of a triangular prism is:

SA = 2(base)+(perimeter)(height)

$SA = 2\left(\frac{1}{2}\right)(l)(w) + (l+w+y)(h)$

SA = (l)(w) + (l+w+y)(h)

Where is the length of the base, is the width of the base, is the hypotenuse of the base, and is the height of the prism

Use the formula for a 45-45-90 triangle to find the length of the hypotenuse:

$a-a-a\sqrt{2}$

$8m-8m-8\sqrt{2}m$

Plugging in our values, we get:

$SA = (8m)(8m) + (8m+8m+8\sqrt{2}m)(12m)$

$SA = 256m^2 + 96\sqrt{2}m^2$

Report an Error

Example Question #3 : Non Cubic Prisms

Find the surface area of the following triangular prism.

Triangular_prism

Possible Answers:

$216 + 216\sqrt{3}m^2$

$216 + 16\sqrt{3}m^2$

$218 + 16\sqrt{3}m^2$

$216 + 18\sqrt{3}m^2$

$18 + 18\sqrt{3}m^2$

Correct answer:

$216 + 18\sqrt{3}m^2$

Explanation:

The formula for the surface area of an equilateral, triangular prism is:

SA = 2(base)+(perimeter)(height)

$SA = 2\left(\frac{s^2\sqrt{3}}{4}\right)+(3s)(h)$

Where is the length of the triangle side and is the length of the height.

Plugging in our values, we get:

$SA = 2\left(\frac{(6m)^2\sqrt{3}}{4}\right)+(3)(6m)(12m)$

$SA = 216 + 18\sqrt{3}m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Prism

David wants to paint the walls in his bedroom. The floor is covered by a $10\ ft \times 16\ ft$ carpet. The ceiling is $8\ ft$ tall. He selects a paint that will cover $75\ ft^2$ per quart and $300\ ft^2$ per gallon. How much paint should he buy?

Possible Answers:

2 gallons and 1 quart

1 gallon

3 quarts

1 gallon and 2 quarts

1 gallon and 1 quart

Correct answer:

1 gallon and 2 quarts

Explanation:

Find the surface area of the walls: SA_walls = 2lh + 2wh, where the height is 8 ft, the width is 10 ft, and the length is 16 ft.

This gives a total surface area of 416 ft². One gallon covers 300 ft², and each quart covers 75 ft², so we need 1 gallon and 2 quarts of paint to cover the walls.

Report an Error

Example Question #1 : Non Cubic Prisms

A box is 5 inches long, 5 inches wide, and 4 inches tall. What is the surface area of the box?

Possible Answers:

$130\ in^2$

$120\ in^2$

$140\ in^2$

$100\ in^2$

$25\ in^2$

Correct answer:

$130\ in^2$

Explanation:

The box will have six total faces: an identical "top and bottom," and identical "left and right," and an identical "front and back." The total surface area will be the sum of these faces.

Since the six faces consider of three sets of pairs, we can set up the equation as:

$SA=2(\text{top})+2(\text{left})+2(\text{front})$

Each of these faces will correspond to one pair of dimensions. Multiply the pair to get the area of the face.

SA=2(lw)+2(wh)+2(lh)

Substitute the values from the question to solve.

SA=2(5*5)+2(5*4)+2(5*4)

SA=50+40+40

$SA=130\ in^2$

Report an Error

Example Question #1 : Non Cubic Prisms

What is the surface area of a rectangular brick with a length of 12 in, a width of 8 in, and a height of 6 in?

Possible Answers:

$576\ in^2$

None of the answers are correct

$432\ in^2$

$216\ in^2$

$382\ in^2$

Correct answer:

$432\ in^2$

Explanation:

The formula for the surface area of a rectangular prism is given by:

SA = 2LW + 2WH + 2HL

SA = 2(12 * 8) + 2(8 * 6) + 2(6 * 12)

SA = 2(96) + 2(48) + 2(72)

SA = 192 + 96 + 144

SA = 432 in²

216 in² is the wrong answer because it is off by a factor of 2

576 in³ is actually the volume, V = L * W * H

Report an Error

Example Question #3 : Non Cubic Prisms

What is the surface area of an equilateral triangluar prism with edges of 6 in and a height of 12 in?

Let $\sqrt{3}=1.732$ and $\sqrt{2}=1.414$ .

Possible Answers:

$189.239\ in^{2}$

$268.732\ in^{2}$

$165.135\ in^{2}$

$247.176\ in^{2}$

$216.414\ in^{2}$

Correct answer:

$247.176\ in^{2}$

Explanation:

The surface area of the prism can be broken into three rectangular sides and two equilateral triangular bases.

The area of the sides is given by: $A=lw=12\cdot 6=72\ in^{2}$ , so for all three sides we get $\dpi{100} 216\ in^{2}$ .

The equilateral triangle is also an equiangular triangle by definition, so the base has congruent sides of 6 in and three angles of 60 degrees. We use a special right traingle to figure out the height of the triangle: 30 - 60 - 90. The height is the side opposite the 60 degree angle, so it becomes $3\sqrt{3}$ or 5.196.

The area for a triangle is given by $A=\frac{1}{2}bh$ and since we need two of them we get $A=bh=6\cdot 3\sqrt{3}=31.176\ in^{2}$ .

Therefore the total surface area is $216\ in^{2}+31.176\ in^{2}=247.176\ in^{2}$ .

Report an Error

View Tutors

Daniel
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Psychology.

View Tutors

Waren
Certified Tutor

Laguna State Polytechnic University, Master of Science, Science Technology.

View Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in San Francisco-Bay Area, SSAT Tutors in Washington DC, Spanish Tutors in Boston, Reading Tutors in Miami, Statistics Tutors in Dallas Fort Worth, Algebra Tutors in Dallas Fort Worth, SAT Tutors in Atlanta, SSAT Tutors in Los Angeles, Spanish Tutors in Washington DC, Biology Tutors in Atlanta

Popular Courses & Classes

LSAT Courses & Classes in New York City, SAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Atlanta, Spanish Courses & Classes in New York City, GMAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Los Angeles, MCAT Courses & Classes in Denver, SAT Courses & Classes in Phoenix, ISEE Courses & Classes in Miami, ACT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SAT Test Prep in Washington DC, ISEE Test Prep in Miami, MCAT Test Prep in New York City, GRE Test Prep in New York City, GMAT Test Prep in Chicago, GMAT Test Prep in Seattle, SSAT Test Prep in New York City, SAT Test Prep in Phoenix, ISEE Test Prep in New York City, ISEE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Non-Cubic Prisms

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Prisms

Example Question #82 : Solid Geometry

Example Question #2 : Non Cubic Prisms

Example Question #3 : Non Cubic Prisms

Example Question #1 : How To Find The Surface Area Of A Prism

Example Question #3 : Non Cubic Prisms

Example Question #1 : How To Find The Surface Area Of A Prism

Example Question #1 : Non Cubic Prisms

Example Question #1 : Non Cubic Prisms

Example Question #3 : Non Cubic Prisms

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: