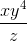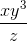All High School Math Resources
Example Questions
Example Question #2 : Polynomials
Simplify the following polynomial function:
First, multiply the outside term with each term within the parentheses:
Rearranging the polynomial into fractional form, we get:
Example Question #1 : Solving Logarithms
You are given that 

Which of the following is equal to 
Since 


Example Question #21 : Pre Calculus
Example Question #22 : Functions And Graphs
What is 
Recall that by definition a logarithm is the inverse of the exponential function. Thus, our logarithm corresponds to the value of 

We know that 

Example Question #1 : Simplifying Logarithms
Solve for 
The correct solution set is not included among the other choices.
The correct solution set is not included among the other choices.
FOIL:
These are our possible solutions. However, we need to test them.
:
The equation becomes 


However, negative numbers do not have logarithms, so this equation is meaningless. 

Example Question #1 : Exponential And Logarithmic Functions
Example Question #1 : Sequences And Series
Evaluate:
None of the other answers are correct.
This sum can be determined using the formula for the sum of an infinite geometric series, with initial term 

Example Question #1 : Sequences And Series
The fourth term in an arithmetic sequence is -20, and the eighth term is -10. What is the hundredth term in the sequence?
55
210
110
220
105
220
An arithmetic sequence is one in which there is a common difference between consecutive terms. For example, the sequence {2, 5, 8, 11} is an arithmetic sequence, because each term can be found by adding three to the term before it.
Let 

We are given the 4th and 8th terms in the sequence, so we can write the following equations:

We now have a system of two equations with two unknowns:
Let us solve this system by subtracting the equation 


This means that d = 2.5.
Using the equation 
Ultimately, we are asked to find the hundredth term of the sequence.
The answer is 220.
Example Question #1 : Sequences And Series
Find the sum, if possible:
The formula for the summation of an infinite geometric series is

where 

Plugging in our values, we get:
Example Question #2 : Sequences And Series
Find the sum, if possible:
The formula for the summation of an infinite geometric series is

where 

Because the terms switch sign, we know that the rate must be negative.
Plugging in our values, we get:
All High School Math Resources











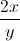

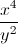
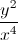





















![\log_{2} \left[ \left ( x+4 \right )\left ( x+5 \right ) \right ] = \log_{2} 6](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/99587/gif.latex)