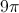Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Cylinders

This figure is a right cylinder with radius of 2 m and a height of 10 m.

What is the surface area of the right cylinder (m²)?

Possible Answers:

62.83

25.14

125.66

125.71

150.80

Correct answer:

150.80

Explanation:

In order to find the surface area of a right cylinder you must find the area of both bases (the circles on either end) and add them to the lateral surface area. The area of the two circles is easy to find with but remember to multiply by 2 for both bases

$2\cdot2^{2}\cdot\pi= 25.14$ .

Next find the lateral area. The lateral area if unrounded would be a rectangle with height of 10 m and length equal to the circumference of the base circles. Thus the lateral area is

$4\cdot\pi\cdot10= 125.66$

Now add the lateral area to the area of the two bases:

25.14 +125.66=150.80

Report an Error

Example Question #2 : Cylinders

Find the surface area of a cylinder given that its radius is 2 and its height is 3.2.

Possible Answers:

20.8

$8\pi$

$20.8\pi$

$12.8\pi$

Correct answer:

$20.8\pi$

Explanation:

The standard equation to find the surface area of a cylinder is

$Surface\ Area=2\pi r^2+2\pi rh$

where denotes the radius and denotes the height.

Plug in the given values for and to find the area of the cylinder:

$Area=2\pi (2)^2+2\pi (2)(3.2)=8\pi +12.8\pi =20.8\pi$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Cylinder

The base of a cylinder has an area of $9\pi$ and the cylinder has a height of . What is the surface area of this cylinder?

Possible Answers:

$90\pi$

$18\pi$

$72\pi$

Correct answer:

$90\pi$

Explanation:

The standard equation for the surface area of a cylinder is

$SA=2\pi r^2+2\pi rh$

where denotes radius and denotes height. We've been given the height in the question, so all we're missing is the radius. However, we are able to find the radius from the area of the circle:

$Area=\pi r^2$

We know the area is $9\pi$

$9\pi =\pi r^2$ so r=3

Now that we have both and , we can plug them into the standard equation for the surface area of a cylinder:

$SA=2\pi (3)^2+2\pi (3)(12)=18\pi +72\pi =90\pi$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Cylinder

Find the surface area of the following cylinder.

Cylinder

Possible Answers:

$246 \pi m^2$

$252 \pi m^2$

$260 \pi m^2$

$240 \pi m^2$

$256 \pi m^2$

Correct answer:

$252 \pi m^2$

Explanation:

The formula for the surface area of a cylinder is:

$SA = lateral\ area + 2\cdot (base)$

$SA = 2 \pi r (h) + 2 (\pi r^2)$

where is the radius of the base and is the length of the height.

Plugging in our values, we get:

$SA = 2 \pi (7m) (11m) + 2 \pi (7m)^2$

$SA = 154 \pi m^2 + 98 \pi m^2 = 252 \pi m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Cylinder

Find the surface area of the following cylinder.

Cylinder

Possible Answers:

$114 \pi m^2$

$104 \pi m^2$

$124 \pi m^2$

$94 \pi m^2$

$84 \pi m^2$

Correct answer:

$104 \pi m^2$

Explanation:

The formula for the surface area of a cylinder is:

SA = 2(base)+(circumference)(height)

$SA = 2(\pi r^2)+(2 \pi r h)$

Where is the radius of the cylinder and is the height of the cylinder

Plugging in our values, we get:

$SA = 2\pi (4m)^2 + 2 \pi (4m)(9m)$

$SA = 104 \pi m^2$

Report an Error

Example Question #2 : Cylinders

Find the surface area of the following partial cylinder.

Cylinder_sector

Possible Answers:

$\frac{104 \pi m^2}{3} + 80m^2$

$\frac{80 \pi m^2}{3} + 144m^2$

$144 \pi m^2+ 80m^2$

$\frac{144 \pi m^2}{6} + 80m^2$

$\frac{144 \pi m^2}{2} + 80m^2$

Correct answer:

$\frac{104 \pi m^2}{3} + 80m^2$

Explanation:

The formula for the surface area of this partial cylinder is:

SA = 2(base)(part)+2(face)+(circumference)(part)(height)

$SA = 2(\pi r^2)(part)+2(r)(h)+(2 \pi r)(part)(h)$

Where is the radius of the cylinder, is the height of the cylinder, and part is the sector of the cylinder.

Plugging in our values, we get:

$SA = 2(\pi (8m)^2)\left(\frac{60}{360}\right)+2(8m)(5m)+(2 \pi (8m))\left(\frac{60}{360}\right)(5m)$

$SA = \frac{64 \pi m^2}{3} + 80m^2 + \frac{40 \pi m^2}{3}$

$SA = \frac{104 \pi m^2}{3} + 80m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Cylinder

Find the surface area of the following partial cylinder.

Partial_cylinder

Possible Answers:

$200 \pi m^2 + 240m^2$

$234 \pi m^2 + 234m^2$

$240 \pi m^2 + 240m^2$

$234 \pi m^2 + 200m^2$

$234 \pi m^2 + 240m^2$

Correct answer:

$234 \pi m^2 + 240m^2$

Explanation:

The formula for the surface area of this partial cylinder is:

SA = 2(base)(part)+2(face)+(circumference)(part)(height)

$SA = 2(\pi r^2)(part)+2(r)(h)+(2 \pi r)(part)(h)$

where is the radius of the cylinder, is the height of the cylinder, and part is the sector of the cylinder.

Plugging in our values, we get:

$SA = 2(\pi r^2)(part)+2(r)(h)+(2 \pi r)(part)(h)$

$SA = 2(\pi (6m)^2)\left(\frac{270}{360}\right)+2(6m)(20m)+(2\pi (6m))\left(\frac{270}{360}\right)(20m)$

$SA = 54 \pi m^2 + 240m^2 +180 \pi m^2$

$SA = 234 \pi m^2 + 240m^2$

Report an Error

Example Question #1 : Cylinders

What is the surface area of cylinder with a radius of 3 and height of 7?

Possible Answers:

$63\pi$

$51\pi$

$10\pi$

$21\pi$

Correct answer:

$51\pi$

Explanation:

The surface area of a cylinder can be determined by the following equation:

$SA=2\pi rh+\pi r^2$

$SA=(2\pi)(3)(7)+\pi(3^2)$

$SA=42\pi+9\pi=51\pi$

Report an Error

Example Question #1 : Cylinders

What is the volume of a cylinder with a radius of 2 and a length that is three times as long as its diameter?

Possible Answers:

$48\pi$

$16\pi$

$12\pi$

Correct answer:

$48\pi$

Explanation:

The volume of a cylinder is the base multiplied by the height or length. The base is the area of a circle, which is $\pi r^{2}$ . Here, the radius is 2. The diameter is 4. Three times the diameter is 12. The height or length is 12. So, the answer is $48\pi$ .

Report an Error

Example Question #1 : Cylinders

A water glass has the shape of a right cylinder. The glass has an interior radius of 2 inches, and a height of 6 inches. The glass is 75% full. What is the volume of the water in the glass (in cubic inches)?

Possible Answers:

$9 \pi$

$36 \pi$

$12 \pi$

$18 \pi$

$24 \pi$

Correct answer:

$18 \pi$

Explanation:

The volume of a right cylinder with radius r=2 and height h=6 is:

$\pi r^2 h = \pi (2)^2 (6) = 24 \pi$

Since the glass is only 75% full, only 75% of the interior volume of the glass is occupied by water. Therefore the volume of the water is:

$24 \pi \times ( 75 / 100 ) = 24 \pi (0.75) = 18 \pi$

Report an Error

View Tutors

Allison
Certified Tutor

Asbury University, Bachelor of Education, Mathematics Teacher Education.

View Tutors

Sarah
Certified Tutor

University of Houston, Bachelors, Psychology.

View Tutors

Shrikar
Certified Tutor

University of South Florida-Main Campus, Bachelor of Science, Biomedical Sciences.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Philadelphia, Calculus Tutors in San Diego, ACT Tutors in Denver, SAT Tutors in Denver, LSAT Tutors in Seattle, ISEE Tutors in San Francisco-Bay Area, Math Tutors in Los Angeles, MCAT Tutors in Chicago, ISEE Tutors in Denver, SSAT Tutors in Philadelphia

Popular Courses & Classes

GMAT Courses & Classes in Atlanta, SAT Courses & Classes in Seattle, LSAT Courses & Classes in Atlanta, SSAT Courses & Classes in Los Angeles, ACT Courses & Classes in Los Angeles, ISEE Courses & Classes in Philadelphia, MCAT Courses & Classes in Phoenix, ISEE Courses & Classes in Denver, ACT Courses & Classes in Chicago, GRE Courses & Classes in Miami

Popular Test Prep

SAT Test Prep in Seattle, LSAT Test Prep in Chicago, GRE Test Prep in Dallas Fort Worth, LSAT Test Prep in San Diego, ACT Test Prep in Los Angeles, ISEE Test Prep in Chicago, ISEE Test Prep in Philadelphia, ACT Test Prep in Chicago, GRE Test Prep in Washington DC, LSAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Cylinders

Example Question #2 : Cylinders

Example Question #1 : How To Find The Surface Area Of A Cylinder

Example Question #1 : How To Find The Surface Area Of A Cylinder

Example Question #1 : How To Find The Surface Area Of A Cylinder

Example Question #2 : Cylinders

Example Question #1 : How To Find The Surface Area Of A Cylinder

Example Question #1 : Cylinders

Example Question #1 : Cylinders

Example Question #1 : Cylinders

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: