All High School Math Resources
Example Questions
Example Question #17 : Algebra Ii
Find the 
Possible Answers:
Correct answer:
Explanation:
To find the 

To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
Now we must set up our two scenarios:

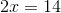

All High School Math Resources
Popular Subjects
GMAT Tutors in San Diego, Chemistry Tutors in Chicago, SAT Tutors in Atlanta, GMAT Tutors in Boston, Physics Tutors in Denver, Algebra Tutors in Houston, SAT Tutors in Dallas Fort Worth, English Tutors in Miami, ACT Tutors in New York City, Physics Tutors in Miami
Popular Courses & Classes
SSAT Courses & Classes in New York City, SAT Courses & Classes in Atlanta, GMAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in San Diego, SSAT Courses & Classes in Atlanta, GMAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Washington DC, ACT Courses & Classes in San Diego, Spanish Courses & Classes in Phoenix
Popular Test Prep
ISEE Test Prep in Washington DC, ACT Test Prep in Washington DC, ISEE Test Prep in Dallas Fort Worth, SSAT Test Prep in Dallas Fort Worth, LSAT Test Prep in San Diego, ISEE Test Prep in San Francisco-Bay Area, GMAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Seattle, GMAT Test Prep in Washington DC
















