All High School Math Resources
Example Questions
Example Question #1 : Understanding Functional Notations
If 





Thus 
Example Question #11 : Introduction To Functions
Let 


Calculate 

Example Question #11 : Functions And Graphs
Evaluate 


Undefined
This expression is the same as saying "take the answer of 

First, we need to find 



Now we take this answer and plug it into 
We can find the value of 


This is our final answer.
Example Question #12 : Functions And Graphs
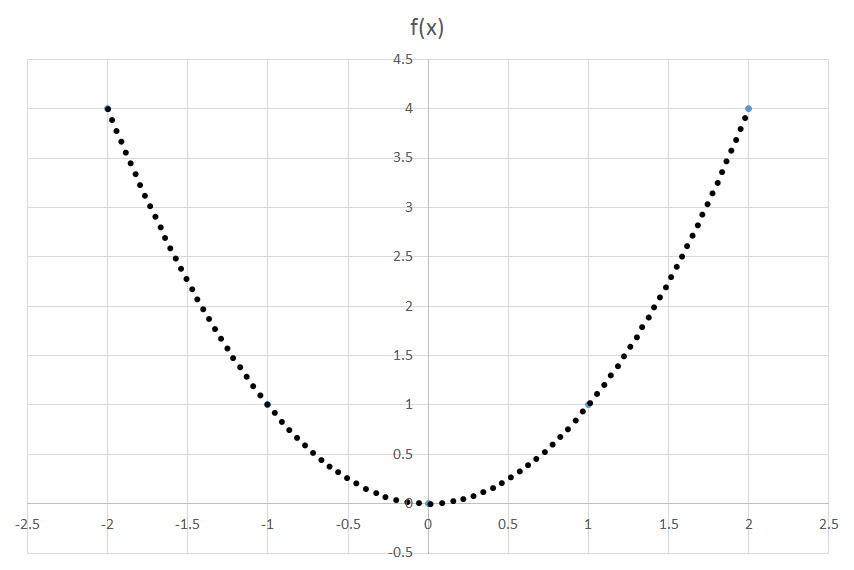
If the function 

Example Question #1 : Understanding Inverse Functions
Let 

We are asked to find 
In order to find the inverse, the first thing we want to do is replace f(x) with y. (This usually makes it easier to separate x from its function.).
Next, we will swap x and y.
Then, we will solve for y. The expression that we determine will be equal to 
Subtract 5 from both sides.
Multiply both sides by -1.
We need to raise both sides of the equation to the 1/3 power in order to remove the exponent on the right side.
We will apply the general property of exponents which states that 
Laslty, we will subtract one from both sides.
The expression equal to y is equal to the inverse of the original function f(x). Thus, we can replace y with 
The answer is 
Example Question #373 : Algebra Ii
What is the inverse of 
The inverse of 




Then solve for 
Example Question #1 : Understanding Inverse Functions
If 

To find the inverse of a function, exchange the 


Certified Tutor
Certified Tutor
All High School Math Resources


























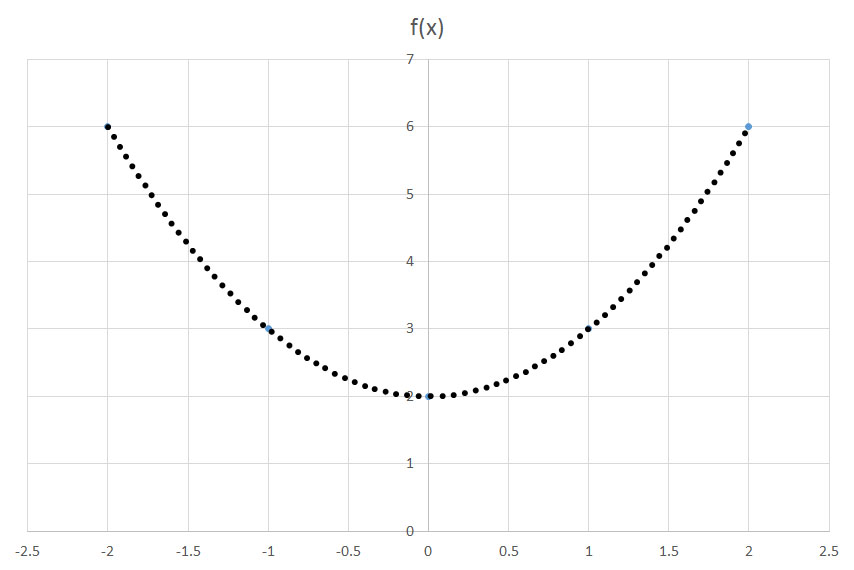
 shifts a function f(x)
shifts a function f(x)  units to the left. Conversely,
units to the left. Conversely,  shifts a function f(x)
shifts a function f(x)  units to the right. In this question, we are translating the graph two units to the left.
units to the right. In this question, we are translating the graph two units to the left. or
or  .
.































