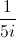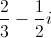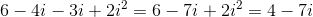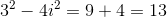Call Now to Set Up Tutoring:

(888) 888-0446

GRE Subject Test: Math : GRE Subject Test: Math

Study concepts, example questions & explanations for GRE Subject Test: Math

Create An Account

All GRE Subject Test: Math Resources

2 Diagnostic Tests 148 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Operations On Complex Numbers

$\sqrt{-70}\cdot -\sqrt{-50}$

Possible Answers:

$5\sqrt{10}$

$-5\sqrt{5}$

$10\sqrt{35}$

$5\sqrt{20}$

$10\sqrt{30}$

Correct answer:

$10\sqrt{35}$

Explanation:

$\sqrt{-70}\cdot -\sqrt{-50}$

Take out i (the square root of -1) from both radicals, simplify, and then multiply. You are not allowed to first multiply the radicals and then simplify because the roots are negative.

$i\sqrt{70}\cdot -i\sqrt{50}$

$i\sqrt{70}\cdot -i\sqrt{25\cdot 2}$

$i\sqrt{70}\cdot -5i\sqrt{2}$

$-5i^{2}\sqrt{140}$

$-5(-1)\sqrt{140}$

$5\sqrt{140}$

$5\sqrt{4\cdot 35}$

$10\sqrt{35}$

Report an Error

Example Question #31 : Imaginary Numbers & Complex Functions

$\sqrt{-225}\cdot \sqrt{-289}$

Possible Answers:

25i

255i

$-15\sqrt{17}$

$15i\sqrt{17}$

Correct answer:

Explanation:

$\sqrt{-225}\cdot \sqrt{-289}$

Take out i (the square root of -1) from both radicals, simplify, and then multiply. You are not allowed to first multiply the radicals and then simplify because the roots are negative.

$i\sqrt{225}\cdot i\sqrt{289}$

$15i\cdot 17i$

$255i^{2}$

255(-1)

Report an Error

Example Question #31 : Imaginary Numbers & Complex Functions

$\sqrt{-15}\cdot \sqrt{-33}$

Possible Answers:

$i\sqrt{495}$

$-\sqrt{495}$

$\sqrt{495}$

$-i\sqrt{495}$

$-3\sqrt{55}$

Correct answer:

$-3\sqrt{55}$

Explanation:

$\sqrt{-15}\cdot \sqrt{-33}$

Take out i (the square root of -1) from both radicals and then multiply. You are not allowed to first multiply the radicals and then simplify because the roots are negative.

$i\sqrt{15}\cdot i\sqrt{33}$

$i^{2}\sqrt{495}$

$(-1)\sqrt{495}$

It might be difficult to tell that this simplifies but you should always check if the perfect squares (4, 9, 16, etc) divide into this number. 9 does divide into 495 so this simplifies further.

$-\sqrt{9\cdot 55}$

$-3\sqrt{55}$

Report an Error

Example Question #281 : Gre Subject Test: Math

$-\sqrt{121}\cdot \sqrt{-12}$

Possible Answers:

$-44\sqrt{3}$

$-22i\sqrt{3}$

$44i\sqrt{3}$

$-44i\sqrt{3}$

$11i\sqrt{12}$

Correct answer:

$-22i\sqrt{3}$

Explanation:

$-\sqrt{121}\cdot \sqrt{-12}$

Take out i (the square root of -1) from the radical, simplify each radical, then multiply.

$-\sqrt{121}\cdot i\sqrt{12}$

$-11\cdot i\sqrt{4\cdot 3}$

$-11\cdot 2i\sqrt{3}$

$-22i\sqrt{3}$

Report an Error

Example Question #1 : Imaginary Numbers

Evaluate $\small \frac{-6+2i}{10-3i}$

Possible Answers:

$\small \small \frac{-66+2i}{91-60i}$

$\small \small \frac{-54+38i}{91-60i}$

$\small \frac{-54+38i}{109}$

$\small \frac{-66+2i}{109}$

You cannot divide by complex numbers

Correct answer:

$\small \frac{-66+2i}{109}$

Explanation:

To divide by a complex number, we must transform the expression by multiplying it by the complex conjugate of the denominator over itself. In the problem, $\small 10-3i$ is our denominator, so we will multiply the expression by $\small \frac{10+3i}{10+3i}$ to obtain:

$\small \frac{-6+2i}{10-3i}\frac{10+3i}{10+3i}=\frac{-60+20i-18i+6i^2}{100-30i+30i-9i^2}$ .

We can then combine like terms and rewrite all $\small i^2$ terms as $\small -1$ . Therefore, the expression becomes:

$\small \frac{-60+2i+6i^2}{100-9i^2}=\frac{-66+2i}{109}$

Our final answer is therefore $\small \frac{-66+2i}{109}$

Report an Error

Example Question #31 : Imaginary Numbers & Complex Functions

Simplify:

$\frac{5-2i}{4-i}$

Possible Answers:

6+3i

18-9i

$\frac{22-3i}{17}$

$\frac{5i+6}{6}$

Correct answer:

$\frac{22-3i}{17}$

Explanation:

To get rid of the fraction, multiply the numerator and denominator by the conjugate of the denominator.

$\frac{5-2i}{4-i}\left(\frac{4+i}{4+i}\right)$

Now, multiply and simplify.

$\frac{5-2i}{4-i}\left(\frac{4+i}{4+i}\right)=\frac{20+5i-8i-2i^2}{16-i^2}$

Remember that i^2=-1

$\frac{20+5i-8i-2i^2}{16-i^2}=\frac{20-3i-2(-1)}{16-(-1)}=\frac{22-3i}{17}$

Report an Error

Example Question #1 : Complex Conjugates

Simplify:

$\frac{8-3i}{2-i}$

Possible Answers:

10-7i

$\frac{19+2i}{5}$

3i+6

$\frac{7+2i}{3}$

Correct answer:

$\frac{19+2i}{5}$

Explanation:

To get rid of the fraction, multiply the numerator and denominator by the conjugate of the denominator.

$\frac{8-3i}{2-i}\left(\frac{2+i}{2+i}\right)$

Now, multiply and simplify.

$\frac{8-3i}{2-i}\left(\frac{2+i}{2+i}\right)=\frac{16+8i-6i-3i^2}{4-i^2}$

Remember that i^2=-1

$\frac{16+8i-6i-3i^2}{4-i^2}=\frac{16+2i-3(-1)}{4-(-1)}=\frac{19+2i}{5}$

Report an Error

Example Question #101 : Classifying Algebraic Functions

Divide: $\frac{2-i}{3+2i}$

The answer must be in standard form.

Possible Answers:

$\frac{2}{3}-\frac{1}{2}i$

$\frac{4}{13}-\frac{7i}{13}$

$\frac{1}{5i}$

$\frac{2}{3}i$

Correct answer:

$\frac{4}{13}-\frac{7i}{13}$

Explanation:

Multiply both the numerator and the denominator by the conjugate of the denominator which is 3-2i which results in

$\frac{\left ( 2-i \right )\left ( 3-2i \right )}{\left ( 3+2i \right )\left ( 3-2i \right )}$

The numerator after simplification give us $6-4i-3i+2i^{2}=6-7i+2i^{2}=4-7i$

The denominator is equal to $3^{2}-4i^{2}=9+4=13$

Hence, the final answer in standard form =

$\frac{4}{13}-\frac{7i}{13}$

Report an Error

Example Question #102 : Classifying Algebraic Functions

$What\ is\ the\ complex\ conjugate\ for\ 3-i\sqrt{7}?$

Possible Answers:

$-i\sqrt{7}$

$-3-i\sqrt{7}$

$3+i\sqrt{7}$

$i\sqrt{7}$

Correct answer:

$3+i\sqrt{7}$

Explanation:

The definition of a complex conjugate is each of two complex numbers with the same real part and complex portions of opposite sign.

$In\ this\ case\ we\ have\ 3-i\sqrt{7}$

$to\ find\ its'\ complex\ conjugate\ we\ change\ the\ sign\ of\ the\ complex\ part$

$The\ complex\ conjugate\ is: 3+i\sqrt{7}$

Report an Error

Example Question #4 : Complex Conjugates

Which of the following is the complex conjugate of (3+4i) ?

Possible Answers:

(3-4i)^3

(3-4i)

(3+4i)^2

Correct answer:

(3-4i)

Explanation:

The complex conjugate of a complex equation $(a+bi), \{a,b\}\in \mathbb {R}$ is (a-bi) .

The complex conjugate when multiplied by the original expression will also give me a real answer.

The complex conjugate of (3+4i) is (3-4i)

Report an Error

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View Tutors

Mike Bahaa
Certified Tutor

Concordia University-Ann Arbor, Master of Arts Teaching, Mathematics Teacher Education.

View Tutors

Pankaj
Certified Tutor

University of Delhi, Electrical Engineer, Electrical Engineering. Columbia University in the City of New York, Master of Arts...

All GRE Subject Test: Math Resources

2 Diagnostic Tests 148 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Houston, Computer Science Tutors in San Diego, Spanish Tutors in Washington DC, GMAT Tutors in Dallas Fort Worth, MCAT Tutors in San Francisco-Bay Area, ACT Tutors in San Diego, Physics Tutors in San Diego, Biology Tutors in New York City, Algebra Tutors in Miami, MCAT Tutors in Washington DC

Popular Courses & Classes

ISEE Courses & Classes in Atlanta, GRE Courses & Classes in New York City, SSAT Courses & Classes in Denver, SSAT Courses & Classes in Phoenix, GRE Courses & Classes in Philadelphia, ACT Courses & Classes in Washington DC, ISEE Courses & Classes in Houston, ISEE Courses & Classes in Phoenix, SSAT Courses & Classes in Seattle, ACT Courses & Classes in Boston

Popular Test Prep

GMAT Test Prep in Atlanta, SSAT Test Prep in Washington DC, ISEE Test Prep in San Francisco-Bay Area, ACT Test Prep in Washington DC, ACT Test Prep in San Diego, ISEE Test Prep in Denver, ACT Test Prep in Boston, GRE Test Prep in New York City, SSAT Test Prep in Atlanta, ISEE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GRE Subject Test: Math : GRE Subject Test: Math

Study concepts, example questions & explanations for GRE Subject Test: Math

All GRE Subject Test: Math Resources

Example Questions

Example Question #21 : Operations On Complex Numbers

Example Question #31 : Imaginary Numbers & Complex Functions

Example Question #31 : Imaginary Numbers & Complex Functions

Example Question #281 : Gre Subject Test: Math

Example Question #1 : Imaginary Numbers

Example Question #31 : Imaginary Numbers & Complex Functions

Example Question #1 : Complex Conjugates

Example Question #101 : Classifying Algebraic Functions

Example Question #102 : Classifying Algebraic Functions

Example Question #4 : Complex Conjugates

All GRE Subject Test: Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: