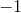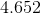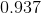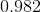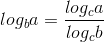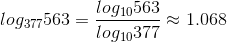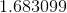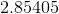Call Now to Set Up Tutoring:

(888) 888-0446

GRE Subject Test: Math : Logarithms

Study concepts, example questions & explanations for GRE Subject Test: Math

Create An Account

All GRE Subject Test: Math Resources

2 Diagnostic Tests 148 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Logarithmic Properties

$Expand: log\left ( \frac{xy}{z} \right )$

Possible Answers:

log(x)-log(y)+log(z)

$\frac{log(x)*log(y)}{log(z)}$

log(x)+log(y)-log(z)

log(x)*log(y)-log(z)

Correct answer:

log(x)+log(y)-log(z)

Explanation:

In order to expand this log, we must remember the log rules.

$Similar\ to\ the\ exponent\ rules\ when\ variables\ are\ multiplied\ within\ a\ log:\\ the\ variables\ are\ added: log(xy)=log(x)+log(y)$

$When\ variables\ are\ divided\ within\ a\ log\ they\ are\ subtracted:\\ log\left ( \frac{x}{y} \right )=log(x)-log(y)$

$For\ this\ problem\ we\ combine\ both\ rules:$

$Expand: log\left ( \frac{xy}{z} \right )=log(x)+log(y)-log(z)$

Report an Error

Example Question #2 : Logarithmic Properties

$Solve\ for\ x: log_{3}(x)=2$

Possible Answers:

$\frac{1}{3}$

Correct answer:

Explanation:

$We\ can\ use\ the\ general\ rule:\ log_{b}(a)=x\\ when\ rewritten\ in\ exponential\ form\ we\ get: b^{x}=a$

$In\ this\ case\ we\ have\ log_{3}(x)=2$

$This\ can\ be\ rewritten\ in\ exponential\ form\ as: 3^2=x$

$We\ know\ that\ 3^2=9;\ so\ x=9$

Report an Error

Example Question #11 : Logarithms

$Rewrite\ as\ one\ log:\ log(a)-(\left log(b)+log(c) \right)$

Possible Answers:

log(a-b-c)

$log\left ( \frac{a}{bc} \right )$

$log\left ( \frac{ab}{c} \right )$

log(a-b+c)

Correct answer:

$log\left ( \frac{a}{bc} \right )$

Explanation:

$When\ condensing\ logs\ we\ must\ remember\ the\ log\ properties:$

$log(x)+log(y)=log(xy): When\ adding;\ we\ multiply.$

$log(x)-log(y)=log\left (\frac{x}{y} \right ): When\ subtracting;\ we\ divide.$

$GIVEN: Rewrite\ as\ one\ log:\ log(a)-(\left log(b)+log(c) \right)\\$

$This\ is\ rewritten\ as:\ log \left (\frac{a}{bc} \right )\\ because\ the\ negative\ will\ be\ distributed\ to\ log(b)\ and\ log(c)$

Report an Error

Example Question #2 : Logarithmic Properties

Rewrite the following expression as a single logarithm

$5log_35x+log_3\frac{1}{4x^3}-log_3x^2$

Possible Answers:

6.06

$log_3\frac{3125x^3}{9}$

$log_3\frac{3125x^3}{4}$

3.076

log_33125x

Correct answer:

6.06

Explanation:

Recall a few properties of logarithms:

1.When adding logarithms of like base, we multiply the inside.

2.When subtracting logarithms of like base, we divide the inside.

3. When multiplying a logarithm by a number, we can raise the inside to that power.

So we begin with this:

$5log_35x+log_3\frac{1}{4x^3}-log_3x^2$

I would start with 3 to simplify the first log.

$log_3(5x)^5+log_3\frac{1}{4x^3}-log_3x^2$

$log_33125x^5+log_3\frac{1}{4x^3}-log_3x^2$

Next, use rule 1 on the first two logs.

$log_3\left(3125x^5\cdot\frac{1}{4x^3}\right)-log_3x^2$

$log_3\left(\frac{3125x^2}{4}\right)-log_3x^2$

Then, use rule 2 to combine these two.

$log_3\left(\frac{3125x^2}{4x^2}\right)=log_3\left(\frac{3125}{4}\right)\approx 6.06$

So our answer is 6.06.

Report an Error

Example Question #1 : Change Of Base

Evaluate:

$3^{3x+3}=27^{2x+2}$

Possible Answers:

$-\frac{1}{2}$

$\frac{2}{3}$

$\frac{1}{2}$

$\frac{4}{13}$

Correct answer:

Explanation:

In order to evaluate the unknown variable, it is necessary to change the base. Looking at the right side of the equation, 27 is equivalent to three cubed.

3^3=27

Therefore, converting the right side of the equation to a base of 3 will allow setting both the left and right side of the exponential terms equal to each other.

$3^{3x+3}=27^{2x+2}$

$3^{3x+3}=3^{3(2x+2)}$

Log both sides to drop the exponents by log properties, and divide the log based 3 on both sides to cancel this term.

Solve for x.

$ln\: 3^(^3^x^+^3^)=ln\:3^3^(^2^x^+^2^)$

3x+3=3(2x+2)

3x+3=6x+6

-3=3x

x=-1

Report an Error

Example Question #2 : Change Of Base

Evaluate the following logarithm:

$log_{377}(563)$

Possible Answers:

1.068

4.652

0.982

0.937

1.238

Correct answer:

1.068

Explanation:

The simplest way to evaluate a logarithm that doesn't have base 10 is with change of base formula:

$log_ba=\frac{log_ca}{log_cb}$

So we have

$log_{377}(563)$

$log_{377}563=\frac{log_{10}563}{log_{10}377}\approx1.068$

Report an Error

Example Question #3 : Change Of Base

$Solve\ for\ x: 3^x=23$

Possible Answers:

2.85405

2.73058

1.89205

1.683099

Correct answer:

2.85405

Explanation:

In order to solve a logarithm, we must first rewrite it in log form:

$3^x=23\ written\ in\ log\ form\ is: log_{3}(23)=x$

To solve for x, we must use the Change of Base:

$log_{3}(23)=\frac{log(23)}{log(3)}$

$\frac{log(23)}{log(3)}=2.85405$

This means that:

$3^{2.85405}=23$

Report an Error

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

All GRE Subject Test: Math Resources

2 Diagnostic Tests 148 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in San Diego, SSAT Tutors in Washington DC, LSAT Tutors in Houston, MCAT Tutors in Washington DC, MCAT Tutors in San Diego, GRE Tutors in Los Angeles, GRE Tutors in Dallas Fort Worth, Biology Tutors in San Diego, ACT Tutors in Dallas Fort Worth, SAT Tutors in Washington DC

Popular Courses & Classes

LSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Philadelphia, SAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Atlanta, ACT Courses & Classes in San Diego, SSAT Courses & Classes in San Diego, SAT Courses & Classes in Seattle, GMAT Courses & Classes in Chicago, SSAT Courses & Classes in Boston, GRE Courses & Classes in Washington DC

Popular Test Prep

ISEE Test Prep in Dallas Fort Worth, ACT Test Prep in San Francisco-Bay Area, ACT Test Prep in Boston, GRE Test Prep in New York City, LSAT Test Prep in Miami, GRE Test Prep in Phoenix, SSAT Test Prep in Miami, ACT Test Prep in San Diego, ISEE Test Prep in Philadelphia, ISEE Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GRE Subject Test: Math : Logarithms

Study concepts, example questions & explanations for GRE Subject Test: Math

All GRE Subject Test: Math Resources

Example Questions

Example Question #3 : Logarithmic Properties

Example Question #2 : Logarithmic Properties

Example Question #11 : Logarithms

Example Question #2 : Logarithmic Properties

Example Question #1 : Change Of Base

Example Question #2 : Change Of Base

Example Question #3 : Change Of Base

All GRE Subject Test: Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: