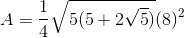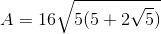GRE Math : Pentagons

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Pentagons

The perimeter of a regular pentagon is 40 units. What is the area of the pentagon?

Possible Answers:

$A=16\sqrt{5(5+2\sqrt{5})}$

$A=\frac{25}{4}\sqrt{5(5+2\sqrt{5})}$

$A=2\sqrt{5(5+2\sqrt{5})}$

$A=8\sqrt{5(5+2\sqrt{5})}$

Correct answer:

$A=16\sqrt{5(5+2\sqrt{5})}$

Explanation:

The formula for the area of a regular pentagon is given by the equation:

$A=\frac{1}{4}\sqrt{5(5+2\sqrt{5})}a^2$

where a is represented by the length of one side. Let's begin by finding the side length of the regular pentagon. If the perimeter is 40, then we can divide by 5 (the number of sides) to find a side length of 8.

If we plug in 8 into the equation:

$A=\frac{1}{4}\sqrt{5(5+2\sqrt{5})}(8)^2$

$A=\frac{1}{4}\sqrt{5(5+2\sqrt{5})}64$

$A=\frac{64}{4}\sqrt{5(5+2\sqrt{5})}$

$A=16\sqrt{5(5+2\sqrt{5})}$

Report an Error

Example Question #51 : Geometry

In a five-sided polygon, one angle measures $105^\circ$ . What are the possible measurements of the other angles?

Possible Answers:

160, 160, 150, 140

145, 155, 160, 155

105, 105, 105, 110

120, 115, 95, 105

115, 95, 110, 120

Correct answer:

120, 115, 95, 105

Explanation:

To find the sum of the interior angles of any polygon, use the formula $(n-2)\cdot 180$ , where n represents the number of sides of a polygon.

In this case:

$(5-2)\cdot 180=540$

The sum of the interior angles will be 540. Go through each answer choice and see which one adds up to 540 (including the original angle given in the problem).

The only one that does is 120, 115, 95, 105 and the original angle of 105.

Report an Error

Example Question #51 : Geometry

In a particular heptagon (a seven-sided polygon) the sum of four equal interior angles, each equal to degrees, is equivalent to the sum of the remaining three interior angles.

Quantity A:

Quantity B: 110

Possible Answers:

The two quantities are equal.

Quantity B is greater

The relationship cannot be determined.

Quantity A is greater.

Correct answer:

Quantity A is greater.

Explanation:

The sum of interior angles in a heptagon is 900 degrees. Note that to find the sum of interior angles of any polygon, it is given by the formula:

(s-2)180 degrees, where is the number of sides of the polygon.

Three interior angles (call them b,c,d ) are unknown, but we are told that the sum of them is equal to the sum of four other equivalent angles (which we'll designate ):

4a=b+c+d

Further more, all of these angles must sum up to 900 degrees:

4a+b+c+d=900

We may not be able to find , , or , indvidually, but the problem does not call for that, and we need only use their relation to , as stated in the first equation with them. Utilizing this in the second, we find:

4a+4a=900

$a=\frac{900}{8}=112.5$

Report an Error

Example Question #3 : How To Find An Angle In A Pentagon

Pentagon2

What is the value of in the figure above?

Possible Answers:

97.5

210

195

105

Correct answer:

97.5

Explanation:

Always begin working through problems like this by filling in all available information. We know that we can fill in two of the angles, giving us the following figure:

Pentagon2 2

Now, we know that for any polygon, the total number of degrees in the figure can be calculated by the equation:

d = 180 *(s-2) , where is the number of sides.

Thus, for our figure, we have:

d = 180 * 3 = 540

Based on this, we know:

540 = 110+50 - a + 135 + a + 50 + 2a

Simplifying, we get:

540 = 345 + 2a

Solving for , we get:

195 = 2a or a = 97.5

Report an Error

Example Question #4 : How To Find An Angle In A Pentagon

Pentagon1

Quantity A: The measure of the largest angle in the figure above.

Quantity B: 120

Which of the following is true?

Possible Answers:

The relationship cannot be determined.

Quantity B is larger.

The two quantities are equal.

Quantity A is larger.

Correct answer:

Quantity A is larger.

Explanation:

Pentagon1

To begin, recall that the total degrees in any figure can be calculated by:

d = 180 * (s-2) , where represents the total number of sides. Thus, we know for our figure that:

d = 3*180 = 540

Now, based on our figure, we can make the equation:

a+2a+3a+120+80 = 540

Simplifying, we get:

6a = 340 or a = 56.6666666666666....

This means that is 170 . Quantity A is larger.

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Chicago, ISEE Tutors in Chicago, Spanish Tutors in Dallas Fort Worth, Physics Tutors in Philadelphia, Algebra Tutors in Boston, Spanish Tutors in Los Angeles, French Tutors in Denver, Math Tutors in Dallas Fort Worth, GRE Tutors in Boston, French Tutors in San Diego

Popular Courses & Classes

GMAT Courses & Classes in Washington DC, Spanish Courses & Classes in Houston, LSAT Courses & Classes in Washington DC, LSAT Courses & Classes in Philadelphia, GRE Courses & Classes in Atlanta, ISEE Courses & Classes in Houston, GRE Courses & Classes in Philadelphia, Spanish Courses & Classes in New York City, SAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Miami

Popular Test Prep

SAT Test Prep in Dallas Fort Worth, SAT Test Prep in Boston, GRE Test Prep in Chicago, GRE Test Prep in Atlanta, MCAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Philadelphia, LSAT Test Prep in Denver, GMAT Test Prep in Miami, SSAT Test Prep in Atlanta, GMAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Pentagons

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : Pentagons

Example Question #51 : Geometry

Example Question #51 : Geometry

Example Question #3 : How To Find An Angle In A Pentagon

Example Question #4 : How To Find An Angle In A Pentagon

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details