All GRE Math Resources
Example Questions
Example Question #1 : How To Find The Length Of The Side Of A Rectangle
A rectangle has an area of 48 and a perimeter of 28. What are its dimensions?
16 x 3
2 x 24
6 x 8
1 x 48
0.25 x 192
6 x 8
We can set up our data into the following two equations:
(Area) LH = 48
(Perimeter) 2L + 2H = 28
Solve the area equation for one of the two variables (here, length): L = 48 / H
Place that value for L into ever place you find L in the perimeter equation: 2(48 / H) + 2H = 28; then simplify:
96/H + 2H = 28
Multiply through by H: 96 + 2H2 = 28H
Get everything on the same side of the equals sign: 2H2 - 28H + 96 = 0
Divide out the common 2: H2 - 14H + 48 = 0
Factor: (H - 6) (H - 8) = 0
Either of these multiples can be 0, therefore, consider each one separately:
H - 6 = 0; H = 6
H - 8 = 0; H = 8
Because this is a rectangle, these two dimensions are the height and width. If you choose 6 for the "height" the other perpendicular dimension would be 8 and vice-versa. Therefore, the dimensions are 6 x 8.
Example Question #1 : Rectangles
The length of a rectangle is three times its width, and the perimeter is 
For any rectangle, 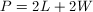



In this problem, we are given that 

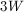
Plug in our value for the perimeter, 
Simplify:
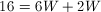
Example Question #2 : Rectangles
The area of a rectangle is 

We know that the following two equations hold for rectangles. For area:
For perimeter:
Now, for our data, we know:
Now, solve the first equation for one of the variables:
Now, substitute this value into the second equation:
Solve for 
Multiply both sides by 
Solve as a quadratic. Divide through by 
Now, get the equation into standard form:
Factor this:
This means that 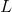



All GRE Math Resources





























