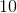If the average of  and  is 70, then their sum is 140.

Likewise, if the average of b and c is 110, then their sum must be 220.

The sum of the first ten scores is 1,200 and the sum of the next 30 scores is 3,000. To take the weighted average of all scores, divide the sum of all scores (4,200) by the total number of scores (40), which would equal 105.

First, pick a distance, preferably one that is divisible by 400 and 600. As an example, we will use 1,200. If the distance is 1,200, then it took 2 hours to get to New York City and 3 hours to get back to San Francisco. So, the plane traveled 2,400 miles in 5 hours. The average speed is simply 2,400 miles divided by 5 hours, which is 480 miles per hour.

The median is the middle number of the data set. If there is an even number of quantities in the data set, take the average of the middle two numbers.

Here, there are 8 numbers, so (18 + 20)/2 = 19. 

The mean, or average, is the sum of the integers divided by number of integers in the set: (20 + 35 + 7 + 12 + 73 + 12 + 18 + 31) / 8 = 26

If we can find the sum of , , and 10, we can determine their average. There is not enough information to solve for  or  individually, but we can find their sum, . 

Write out the average formula for the original three quantities.  Remember, adding together and dividing by the number of quantities gives the average: 

Isolate : 

Write out the average formula for the new three quantities: 

Combine the integers in the numerator:

Replace  with 27:

To solve this problem, calculate Quantity A.

The arithmetic mean for a set of values is the sum of these values divided by the total number of values:

For the set , the mean is

Now recall that we're told that arithmetic mean of a, b, and c is , i.e.

Using this fact, return to what we've written for Quantity A:

Quantity B is also 

So the two quantities are equal.

The key to this problem is to recognize that Quantity A can be rewritten.

The function 

can be written as

Now, recall what we're told about the mean of a and b, namely that it equals .

This is equivalent to saying

From this, we can see that

Therefore, we can find a value for Quantity A:

Quantity A is greater.

All of the multiples of 5 from 5 to 50 are 

.  

The total of all of them is 275.  

Then the mean will be 27.5 

.

In order to solve this problem, we must know how to find the arithmetic mean for a set of numbers. The arithmetic mean is defined as the sum of all the numbers added up divided by the number. In this case, we first have to find the amount of credits present. Adding all the credits up, we find there are 15 credits. Now, by adding up the grades for each of those credits and dividing by the total number of credits, we can solve for the average grade of the student.