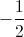GRE Math : Coordinate Geometry

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Lines

What is the slope of the equation -2x+4y=8 ?

Possible Answers:

$-\frac{1}{2}$

$\frac{1}{2}$

Correct answer:

$\frac{1}{2}$

Explanation:

To find the slope of a line, you should convert an equation to the slope-intercept form. In this case, the equation would be $y=\frac{1}{2}x+2$ , which means the slope is $\frac{1}{2}$ .

Report an Error

Example Question #1 : How To Find The Slope Of A Line

What is the slope of the line 3x+2y=5 ?

Possible Answers:

$\small -\frac{3}{2}$

$\small \frac{3}{2}$

$\small \frac{2}{3}$

Correct answer:

$\small -\frac{3}{2}$

Explanation:

To find the slope, put the equation in slope-intercept form $\small (y=mx+b)$ . In this case we have $y=-\frac{3}{2}+5$ , which indicates that the slope is $-\frac{3}{2}$ .

Report an Error

Example Question #2 : How To Find The Slope Of A Line

What is the slope of a line passing through the point (12,-4) , if it is defined by:

y=mx+7 ?

Possible Answers:

$\frac{-1}{7}$

$\frac{-11}{12}$

$\frac{-7}{12}$

$\frac{11}{12}$

$\frac{12}{7}$

Correct answer:

$\frac{-11}{12}$

Explanation:

Since the equation is defined as it is, you know the y-intercept is . This is the point (0,7) . To find the slope of the line, you merely need to use the two points that you have and find the equation:

$\frac{rise}{run}=\frac{-4-7}{12-0}=\frac{-11}{12}$

Report an Error

Example Question #31 : Coordinate Geometry

Line1

Which of the following could be an equation for the red line pictured above?

Possible Answers:

y=5x-4

y=-4x-2

y=15x+12

y=4x+3

y=-3x+3

Correct answer:

y=-3x+3

Explanation:

There are two key facts to register about this drawing. First, the line clearly has a negative slope, given that it runs "downhill" when you look at it from left to right. Secondly, it has a positive y-intercept. Therefore, you know that the coefficient for the term must be negative, and the numerical coefficient for the y-intercept must be positive. This only occurs in the equation y=-3x+3 . Therefore, this is the only viable option.

Report an Error

Example Question #4 : How To Find The Slope Of A Line

What is the slope of a line defined by the equation:

14x-3y+3=10x+4y-10

Possible Answers:

$\frac{4}{7}$

$\frac{7}{10}$

$-\frac{4}{7}$

$-\frac{10}{7}$

$\frac{5}{6}$

Correct answer:

$\frac{4}{7}$

Explanation:

A question like this is actually rather easy. All you need to do is rewrite the equation in slope intercept form, that is:

y=mx+b

Therefore, begin to simplify:

14x-3y+3=10x+4y-10

Becomes...

-3y-4y=10x-14x-10-3

Then...

-7y=-4x-13

Finally, divide both sides by :

$y=\frac{4x}{7}+\frac{13}{7}$

The coefficient for the term is your slope: $\frac{4}{7}$

Report an Error

Example Question #5 : How To Find The Slope Of A Line

What is the slope of line 3 = 8y - 4x?

Possible Answers:

-2

0.5

-0.5

Correct answer:

0.5

Explanation:

Solve equation for y. y=mx+b, where m is the slope

Report an Error

Example Question #221 : Geometry

Find the slope of the line 6X – 2Y = 14

Possible Answers:

-3

-6

Correct answer:

Explanation:

Put the equation in slope-intercept form:

y = mx + b

-2y = -6x +14

y = 3x – 7

The slope of the line is represented by M; therefore the slope of the line is 3.

Report an Error

Example Question #6 : How To Find The Slope Of A Line

If 2x – 4y = 10, what is the slope of the line?

Possible Answers:

–2

–0.5

–5/2

0.5

Correct answer:

0.5

Explanation:

First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.

Report an Error

Example Question #32 : Coordinate Geometry

What is the slope of the line with equation 4x – 16y = 24?

Possible Answers:

1/2

1/8

–1/8

–1/4

1/4

Correct answer:

1/4

Explanation:

The equation of a line is:

y = mx + b, where m is the slope

4x – 16y = 24

–16y = –4x + 24

y = (–4x)/(–16) + 24/(–16)

y = (1/4)x – 1.5

Slope = 1/4

Report an Error

Example Question #31 : Coordinate Geometry

What is the slope of a line which passes through coordinates $\dpi{100} \small (3,7)$ and $\dpi{100} \small (4,12)$ ?

Possible Answers:

$\dpi{100} \small 3$

$\dpi{100} \small \frac{1}{2}$

$\dpi{100} \small \frac{1}{5}$

$\dpi{100} \small 5$

$\dpi{100} \small 2$

Correct answer:

$\dpi{100} \small 5$

Explanation:

Slope is found by dividing the difference in the $\dpi{100} \small y$ -coordinates by the difference in the $\dpi{100} \small x$ -coordinates.

$\dpi{100} \small \frac{(12-7)}{(4-3)}=\frac{5}{1}=5$

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Denver, LSAT Tutors in Washington DC, Spanish Tutors in New York City, SSAT Tutors in New York City, Chemistry Tutors in Washington DC, SAT Tutors in Boston, SSAT Tutors in Washington DC, LSAT Tutors in New York City, Physics Tutors in Washington DC, Reading Tutors in Houston

Popular Courses & Classes

SAT Courses & Classes in Chicago, ACT Courses & Classes in Phoenix, ISEE Courses & Classes in Atlanta, GRE Courses & Classes in Los Angeles, LSAT Courses & Classes in New York City, ACT Courses & Classes in Miami, SAT Courses & Classes in Seattle, GMAT Courses & Classes in Atlanta, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ISEE Test Prep in Dallas Fort Worth, SAT Test Prep in Atlanta, SSAT Test Prep in Los Angeles, LSAT Test Prep in San Diego, LSAT Test Prep in Boston, ACT Test Prep in Miami, MCAT Test Prep in Los Angeles, GRE Test Prep in Denver, LSAT Test Prep in Denver, ACT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Coordinate Geometry

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #31 : Lines

Example Question #1 : How To Find The Slope Of A Line

Example Question #2 : How To Find The Slope Of A Line

Example Question #31 : Coordinate Geometry

Example Question #4 : How To Find The Slope Of A Line

Example Question #5 : How To Find The Slope Of A Line

Example Question #221 : Geometry

Example Question #6 : How To Find The Slope Of A Line

Example Question #32 : Coordinate Geometry

Example Question #31 : Coordinate Geometry

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details