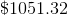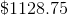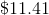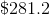All GRE Math Resources
Example Questions
Example Question #1 : How To Find Compound Interest
A five-year bond is opened with 

Each year, you can calculate your interest by multiplying the principle (

For two years, it would be:

Therefore, you can solve for a five year period by doing:
Using your calculator, you can expand the 


Example Question #1 : How To Find Compound Interest
Jack has 



First, break the problem into two segments: the amount Jack invests in the high-yield savings, and the amount Jack invests in the simple interest account (10,000 and 5,000 respectively).
Now let's work with the high-yield savings account. $10,000 is invested at an annual rate of 8%, compounded quarterly. We can use the compound interest formula to solve:
Plug in the values given:
Therefore, Jack makes $824.32 off his high-yield savings account. Now let's calculate the other interest:
Add the two together, and we see that Jack makes a total of, 
Example Question #1 : How To Find Compound Interest
If a cash deposit account is opened with 

It is easiest to break this down into steps. For each year, you will multiply by 
After year 1: 
After year 2: 

After year 3: 

Thus, the positive difference of the interest from the last period and the interest from the first period is:
Example Question #11 : Gre Quantitative Reasoning
Quantitative Comparison
Quantity A: x2
Quantity B: x3
Quantity A is greater.
The relationship cannot be determined from the information given.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined from the information given.
Let's pick numbers. For quantitative comparisons with exponents, it's good to try 0, a negative number, and a fraction.
0: 02 = 0, 03 = 0, so the two quantities are equal.
–1: (–1)2 = 1, (–1)3 = –1, so Quantity A is greater.
Already we have a contradiction so the answer cannot be determined.
Example Question #202 : Exponents
If 
We know that the expression must be negative. Therefore one or all of the terms x7, y8 and z10 must be negative; however, even powers always produce positive numbers, so y8 and z10 will both be positive. Odd powers can produce both negative and positive numbers, depending on whether the base term is negative or positive. In this case, x7 must be negative, so x must be negative. Thus, the answer is x < 0.
Example Question #14 : Gre Quantitative Reasoning
Which quantity is the greatest?
Quantity A

Quantity B
The realationship cannot be determined from the information given.
Quantity A is greater.
The two quantities are equal.
Quantity B is greater.
Quantity A is greater.
First rewrite quantity B so that it has the same base as quantity A.



Now we can compare the two quantities.


Example Question #3 : How To Find Patterns In Exponents
Simplify the following:
With problems like this, it is always best to break apart your values into their prime factors. Let's look at the numerator and the denominator separately:
Numerator
Continuing the simplification:
Now, these factors have in common a 
Denominator
This is much simpler:
Now, return to your fraction:
Cancel out the common factors of 
Example Question #21 : Algebra
What digit appears in the units place when 
This problem is quite simple if you recall that the units place of powers of 2 follows a simple 4-step sequence.
Observe the first few powers of 2:
21 = 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, 26 = 64, 27 = 128, 28 = 256 . . .
The units place follows a sequence of 2, 4, 8, 6, 2, 4, 8, 6, etc. Thus, divide 102 by 4. This gives a remainder of 2.
The second number in the sequence is 4, so the answer is 4.
Example Question #6 : How To Find Patterns In Exponents
Which of the following is a multiple of 
For exponent problems like this, the easiest thing to do is to break down all the numbers that you have into their prime factors. Begin with the number given to you:
Now, in order for you to have a number that is a multiple of this, you will need to have at least 

Example Question #4 : How To Find Patterns In Exponents
Simplify the following:
Because the numbers involved in your fraction are so large, you are going to need to do some careful manipulating to get your answer. (A basic calculator will not work for something like this.) These sorts of questions almost always work well when you isolate the large factors and notice patterns involved. Let's first focus on the numerator. Go ahead and break apart the 
Note that these have a common factor of 
Now, put this back into your fraction:
All GRE Math Resources