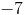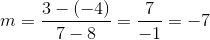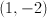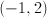GRE Math : Lines

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #41 : Coordinate Geometry

What is the slope of the line represented by the equation $6y-16x=7$ ?

Possible Answers:

$16$

$6$

$-16$

$\frac{8}{3}$

$\frac{7}{6}$

Correct answer:

$\frac{8}{3}$

Explanation:

To rearrange the equation into a $y=mx+b$ format, you want to isolate the $y$ so that it is the sole variable, without a coefficient, on one side of the equation.

First, add $11x$ to both sides to get $6y=7+16x$ .

Then, divide both sides by 6 to get $y=\frac{7+16x}{6}$ .

If you divide each part of the numerator by 6, you get $y=\frac{7}{6}+\frac{16x}{6}$ . This is in a $y=b+mx$ form, and the $m$ is equal to $\frac{16}{6}$ , which is reduced down to $\frac{8}{3}$ for the correct answer.

Report an Error

Example Question #222 : Geometry

What is the slope of the given linear equation?

2x + 4y = -7

Possible Answers:

-2

1/2

-1/2

-7/2

Correct answer:

-1/2

Explanation:

We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)

Report an Error

Example Question #1 : How To Find The Slope Of A Line

What is the slope of the line:

$\frac{14}{3}x=\frac{1}{6}y-7$

Possible Answers:

$\frac{1}{28}$

$-\frac{1}{28}$

Correct answer:

Explanation:

First put the question in slope intercept form (y = mx + b):

–(1/6)y = –(14/3)x – 7 =>

y = 6(14/3)x – 7

y = 28x – 7.

The slope is 28.

Report an Error

Example Question #2 : How To Find The Slope Of A Line

What is the slope of a line that passes though the coordinates $(5,2)$ and $(3,1)$ ?

Possible Answers:

$-\frac{1}{2}$

$\frac{1}{2}$

$4$

$-\frac{2}{3}$

$\frac{2}{3}$

Correct answer:

$\frac{1}{2}$

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{1-2}{3-5}=\frac{-1}{-2}=\frac{1}{2}$

Report an Error

Example Question #41 : Coordinate Geometry

What is the slope of a line running through points (7,3) and (8,-4) ?

Possible Answers:

$\frac{7}{3}$

$-\frac{1}{7}$

Correct answer:

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{3-(-4)}{7-8}=\frac{7}{-1}=-7$

Report an Error

Example Question #11 : Other Lines

Find the point where the line y = .25(x – 20) + 12 crosses the x-axis.

Possible Answers:

(0,–28)

(–28,0)

(0,0)

(–7,0)

(12,0)

Correct answer:

(–28,0)

Explanation:

When the line crosses the x-axis, the y-coordinate is 0. Substitute 0 into the equation for y and solve for x.

.25(x – 20) + 12 = 0

.25x – 5 = –12

.25x = –7

x = –28

The answer is the point (–28,0).

Report an Error

Example Question #41 : Lines

On a coordinate plane, two lines are represented by the equations y=x+3 and y=2x+5 . These two lines intersect at point . What are the coordinates of point ?

Possible Answers:

(2,-1)

(-1,2)

(-2,1)

(1,-2)

(-2,-1)

Correct answer:

(-2,1)

Explanation:

You can solve for the within these two equations by eliminating the . By doing this, you get x+3=2x+5 .

Solve for to get and plug back into either equation to get the value of as 1.

Report an Error

Example Question #42 : Lines

If the two lines represented by y=x+4 and y=3x-8 intersect at point , what are the coordinates of point ?

Possible Answers:

(2,6)

(6,8)

(6,10)

(4,8)

(2,4)

Correct answer:

(6,10)

Explanation:

Solve for by setting the two equations equal to one another:

x+4=3x-8

x=6

Plugging back into either equation gives y=10 .

These are the coordinates for the intersection of the two lines.

Report an Error

Example Question #43 : Lines

Determine the greater quantity:

BD+AC-BC

Possible Answers:

The relationship cannot be determined.

BD+AC-BC

The quantities are equal.

Correct answer:

The quantities are equal.

Explanation:

$\dpi{100} \small BD+AC$ is the length of the line, except that $\dpi{100} \small BC$ is double counted. By subtracting $\dpi{100} \small BC$ , we get the length of the line, or $\dpi{100} \small AD$ .

Report an Error

Example Question #3 : How To Find Out If A Point Is On A Line With An Equation

Which of the following set of points is on the line formed by the equation 3x-6y=12 ?

Possible Answers:

(-1,3)

(-4,-2)

(-2,-4)

(4,0)

(6,0)

Correct answer:

(4,0)

Explanation:

The easy way to solve this question is to take each set of points and put it into the equation. When we do this, we find the only time the equation balances is when we use the points (4,0) .

3x-6y=12

3(4)-6(0)=12

12-0=12

12=12

For practice, try graphing the line to see which of the points fall on it.

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Denver, Computer Science Tutors in Dallas Fort Worth, GMAT Tutors in San Diego, Math Tutors in Dallas Fort Worth, Statistics Tutors in New York City, LSAT Tutors in Miami, Chemistry Tutors in Dallas Fort Worth, ACT Tutors in Chicago, French Tutors in Los Angeles, French Tutors in Atlanta

Popular Courses & Classes

ISEE Courses & Classes in Atlanta, MCAT Courses & Classes in New York City, MCAT Courses & Classes in Boston, GMAT Courses & Classes in San Diego, SSAT Courses & Classes in Phoenix, SSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Los Angeles, GMAT Courses & Classes in New York City, GRE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

MCAT Test Prep in Seattle, GMAT Test Prep in San Diego, GRE Test Prep in Seattle, GMAT Test Prep in New York City, MCAT Test Prep in San Diego, LSAT Test Prep in Denver, ACT Test Prep in Seattle, LSAT Test Prep in San Diego, LSAT Test Prep in Philadelphia, ISEE Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Lines

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #41 : Coordinate Geometry

Example Question #222 : Geometry

Example Question #1 : How To Find The Slope Of A Line

Example Question #2 : How To Find The Slope Of A Line

Example Question #41 : Coordinate Geometry

Example Question #11 : Other Lines

Example Question #41 : Lines

Example Question #42 : Lines

Example Question #43 : Lines

Example Question #3 : How To Find Out If A Point Is On A Line With An Equation

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details