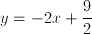All GRE Math Resources
Example Questions
Example Question #2 : How To Find The Slope Of A Perpendicular Line
What is the slope of the line perpendicular to the line given by the equation
6x – 9y +14 = 0
6
-3/2
-1/6
-2/3
2/3
-3/2
First rearrange the equation so that it is in slope-intercept form, resulting in y=2/3 x + 14/9. The slope of this line is 2/3, so the slope of the line perpendicular will have the opposite reciprocal as a slope, which is -3/2.
Example Question #3 : How To Find The Slope Of A Perpendicular Line
What is the slope of the line perpendicular to the line represented by the equation y = -2x+3?
-1/2
2
-2/3
2/3
1/2
1/2
Perpendicular lines have slopes that are the opposite of the reciprocal of each other. In this case, the slope of the first line is -2. The reciprocal of -2 is -1/2, so the opposite of the reciprocal is therefore 1/2.
Example Question #1 : How To Find The Slope Of A Perpendicular Line
Find the slope of a line perpendicular to the line y = –3x – 4.
1/4
4
1/3
–3
1/3
First we must find the slope of the given line. The slope of y = –3x – 4 is –3. The slope of the perpendicular line is the negative reciprocal. This means you change the sign of the slope to its opposite: in this case to 3. Then find the reciprocal by switching the denominator and numerator to get 1/3; therefore the slope of the perpendicular line is 1/3.
Example Question #1 : How To Find The Slope Of A Perpendicular Line
What is the slope of a line perpendicular to the following:
The question puts the line in point-slope form y – y1 = m(x – x1), where m is the slope. Therefore, the slope of the original line is 1/2. A line perpendicular to another has a slope that is the negative reciprocal of the slope of the other line. The negative reciprocal of the original line is –2, and is thus the slope of its perpendicular line.
Example Question #1 : How To Find The Slope Of A Perpendicular Line
A line is defined by the following equation:
What is the slope of a line that is perpendicular to the line above?
The equation of a line is 

Rearrange the equation to match this:
For the perpendicular line, the slope is the negative reciprocal;
therefore
Example Question #13 : Perpendicular Lines
The equation of a particular line is as follows:

What is the slope of a line perpendicuar to this one?
The slope of a perpendicular line is the opposite reciporical of the originial slope.
The opposite would be changing the sign from positive to negative or vice versa.
The reciporical is flipping the fraction or switching the numerator and denominator.
This equation is in slope-intercept form,
meaning m represents the slope of the equation.
Since the original is 

Example Question #91 : Lines
Which of the following equations represents a line perpendicular to 3x + 4y = 5?
y = 3x + 2
y = (-4/3)x + 2
y = (3/4)x - 8
y = (4/3)x - 15
y = 4x - 2
y = (4/3)x - 15
Perpendicular lines have opposite and reciprocal slopes. Therefore, let us find the slope of our line and appropriately modify it to find the perpendicular line. To find the slope of our line, remember that in the slope-intercept form (y = mx + b), m represents the slope.
3x + 4y = 5 => 4y = 5 - 3x => y = (-3/4)x + 5/4
Therefore, the slope of our line is -3/4. The perpendicular to this would be 4 / 3. Therefore, only y = (4/3)x - 15 is perpendicular.
Example Question #92 : Lines
What is the equation for the line passing through the point (5,4) and is perpendicular to the line 8y + 4x = 10?
y = x – 6
y = 3x + 44
y = -0.5x – 6
y = -2x + 15
y = 2x – 6
y = 2x – 6
To solve this, we need to use the point-slope form. However, to do this, we need to ascertain the slope of the perpendicular line. For this, get 8y + 4x = 10 into slope-intercept form:
8y = -4x + 10; y = (-1/2)x + 1.25
Therefore, the slope of this line is -1/2 and its perpendicular (opposite and reciprocal) slope is 2.
The point slope form is: (y – y1) = m * (x – x1)
For our data it is: y – 4 = 2 * (x – 5)
Simplifying, we get: y – 4 = 2 x – 10; y = 2x – 6
Example Question #1 : How To Find The Equation Of A Perpendicular Line
Which of the following is an equation of a line that is perpendicular to 
Rewrite the equation in 
The perpendicular line will have a slope which is the negative reciprocal of the slope 
Example Question #4 : How To Find The Equation Of A Perpendicular Line
Which of the following is a line perpendicular to the line passing through 

To find if something is perpendicular, you need to first know the slope of your given line. Based on your points, this is easy. Recall that slope is merely:
This is:
Since a perpendicular line has a slope that is both opposite in sign and reciprocal, you need to choose a line with a slope of 
All GRE Math Resources