GRE Math : Sectors
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #1 : How To Find The Angle For A Percentage Of A Circle
A study was conducted to determine the effectiveness of a vaccine for the common cold (Rhinovirus sp.). 1000 patients were studied. Of those, 500 received the vaccine and 500 did not. The patients were then exposed to the Rhinovirus and the results were tabulated.
Table 1 shows the number of vaccinated and unvaccinated patients in each age group who caught the cold.
Suppose the scientists wish to create a pie chart reflecting a patient's odds of catching the virus depending on vaccination status and age group.
All 1000 patients are included in this pie chart.
What would be the angle of the arc for the portion of the chart representing vaccinated patients of all age groups who caught the virus?
10°
36°
18°
Insufficient information to answer this question
60°
18°
First, we must determine what proportion of the 1000 patients were vaccinated and caught the virus. The total number of patients who were vaccinated and caught the virus is 50.
18 + 4 + 5 + 4 + 19 = 50
The proportion of the patients is represented by dividing this group by the total number of participants in the study.
50/1000 = 0.05
Next, we need to figure out how that proportion translates into a proportion of a pie chart. There are 360° in a pie chart. Multiply 360° by our proportion to reach the solution.
360° * 0.05 = 18°
The angle of the arc representing vaccinated patients who caught the virus is 18°.
Example Question #32 : Plane Geometry
A group of students ate an 
You will not need all of the information given in the prompt in order to answer this question successfully. You really only need to know that there were 
Example Question #1 : How To Find The Area Of A Sector
If the outer arc of 1/12th of a circular pie is 7π, what is the area of 1/4th of the pie?
21π
441π
10.5π
1764π
None of the other answers
441π
Our initial data tells us that (1/12)c = 7π or (1/12)πd = 7π. This simplifies to (1/12)d = 7 or d = 84. Furthermore, we know that r is 42. Given this, we can ascertain the area of a quarter of the whole pie by taking one fourth of the whole area or 0.25 * π * 422 = 0.25 * 1764 * π = 441π
Example Question #1 : How To Find The Area Of A Sector
What is the area of a sector of a circle of radius 4 that spans an arc of 86 degrees?
1/4 * ∏
172/45 * ∏
17/42 * ∏
12/53 * ∏
1/5 * ∏
172/45 * ∏
sector area = ∏ * r2 * degrees/360 = ∏ * 42 * 86/360 = 172/45 * ∏
Example Question #11 : Sectors
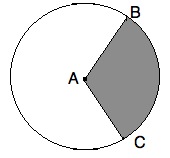
The circle above has a center of A, and points B and C lie on the circumference.
What is the area of the shaded region?
None of the other answers
We need to begin by finding the area of the following sector:
If ∠BAC = 120°, then the area of sector BAC is equal to 120 / 360 = 1/3 of the entire circle. Since AC is 12 and is a radius, we know the total area is pi *122 = 144*pi. The sector is then 144*pi / 3 = 48*pi.
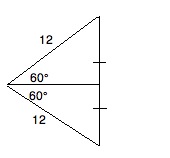
Now, we need to find the area of the triangle ABC. Since AB and AC are equal (both being radii of our circle), we have an icoseles triangle. If we drop a height from ∠BAC, we have the following triangle ABC:
We can use the 30-60-90 rule to find the height and base. One half of the base (x) is found by the following ratio:
√(3) / 2 = x / 12
Solving for x, we get: x = 6 * √(3). Therefore, the base is 12 * √(3).
To find the height (y), we use the following ratio:
1 / 2 = y / 12
Solving for y, we get y = 6.
Therefore, the area of the triangle = 0.5 * 6 * 12 * √(3) = 3 * 12 * √(3) = 36 * √(3)
The area of the shaded region is then 48*pi - 36 * √(3).
All GRE Math Resources
