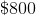One way to solve this is by considering that the increase in taxes is a linear addition of 2%.  Therefore we can ask the question, 2% of what amount yields $150,000?  This can be represented in the following equation:

0.02 * x = 150,000

Solve for x: $7,500,000

Therefore, the total at the old rate is 7,500,000 * 0.06 = $450,000.

To solve this problem, we must understand that we can't simply use the percentage change from 2013-2014 in order to solve this problem. Because the populations change, simply using the percentage change in order to is invalid. Therefore we must find the amount of people that were charming in each year to solve for this problem.

In 2013,  of the  people in America were considered charming, this means that the number of charming people in America in 2013 is   people.

In 2014,  of the  people in America were considered charming, this means that the number of charming people in America in 2014 is   people.

Therefore to find the percent increase of charming people, we simply find the difference in charming people from 2013-2014 and divide by the number of charming people in 2013.   or a  increase in charming people. 

Let  represent the original price of the TV. Now, set up an equation where the discounted price of the TV (10% discount) minus 200 dollars is equal to 65% of the original price of the TV:

Solve for 

The original price of the TV is .

There are two ways to consider the value of B. First, you can subtract 40% from the initial $50 dollars: $50 – 0.4 * $50 = $30. This gives you the value after the markdown. Then to mark up the price, add 50% of $30 to the $30: $30 + 0.5 * $30 = $45.

A shorter way to do this problem is to consider the first markdown as reducing the price to 60% of the original, then considering the markup as making it 150% of the new price.  This can be done in one set of multiplications: $50 * 0.6 * 1.5 = $45.  Either way, the answer is the same. A is the larger quantity.

If we multiply $200 by 0.7, we find the dress has been reduced by $140 on the first discount. Since the dress now costs $60, we multiply that by 0.15 and find the dress has been discounted by an additional $9. The final sale of the dress is $51, with $149 of the original price removed.

Normally, 3 pens cost 3 * .49 = $1.47. Thus, on each set of 3 pens, the sale price saves the customer $1.47 - 99 = 48 cents. Multiply this by 4 to get the savings for 12 pens, and you get .48 * 4 = $1.92.

This is a straightforward percentage problem. After the first discount, the price of the weights is $0.8X. This price is then further reduced by 10% for the employee discount. 90% of 0.8X = 0.9(0.8X) = 0.72X.

The easiest way to solve this is to note that a 30% markdown reduces the cost to 70% of the original cost.  Likewise, a 40% markup is the same as making the price 140% of its current value.  Using this, we can solve our problem in one string of multiplications:

New cost = Original * 0.7 * 1.4 * 0.9

New cost = 20 * 0.7 * 1.4 * 0.9 = 17.64

To find 25% of $50 you multiply 50 and 0.25. This gives you 12.50. This means the dress is $12.50 cheaper, so it now costs 50 – 12.50 = $37.50. You have an additional 10% off, so you multiply 37.50 by 0.10 to get 3.75. 37.50 – 3.75 = $33.75. This is the cost of the dress. NOTE: You CANNOT add 25% and 10% and take 35% off of the $50 dress. You will get the wrong answer. 

To calculate a 30% increase in cost, you can multiply the base cost by 1.3; therefore, if we are going to increase the rate five times, we will multiply by 1.3 five times, which is the same as 1.3⁵. The cost of creating 100 units per hour is 27 * 1.3⁵ = 100.25. 

If we want to make a 25% profit, we can set up the equation:

Price = 1.25 * 100.25 or 125.3125. To make at least a 25%, this will be $125.32.