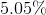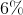For this problem, we are given no numbers to work with. Therefore, we can substitute a number of our choosing into the problem. For simplicities sake, the number chosen will be $100. If the price of water decreased by 10%, that would mean that the new price for water if the old price was $100 is $90. Because tax increased by 5%, that would mean that for a bottle of water, if we assume the old tax rate was 10%, the new tax rate is 10.5%.  This would mean that if previously, if you paid 10% tax for a $100 bottle of water, you would pay $10 in taxes.

Now, you would pay 10.5% tax for a $90 bottle of water meaning you would pay $9.45 in tax.

This problem asks you for the percentage the tax changes by, therefore in order to find the percent change, we divide the new tax by the old tax,  or 94.5%. This means that the amount of tax paid has decreased by 5.5% compared to the following year.

In this problem, we are asked to find the price of  of apples.  The original price of apples is stated to be .  That would mean that  of apples would cost . Because the supermarket gives a  discount if you buy  of apples at once, .  Rounded to the nearest cent, 13 pounds of apples would cost .

Principal = $5000 (original amount)

Interest = 30 months = 2 years and a half

half a year's interest is

Total interest =

The easiest way to do this is to translate the question into "is / of language."  The question is asking, "What percentage of  is ?"  Remember, is means equals and of indicates multiplication.  "What" means a variable like .  Therefore, we can rewrite our sentence as:

Solving for , we get:

This is %.  Rounding to the nearest hudredth, you get  or .

You can solve this by using the standard formula for simple interest (which is merely a derivative of standard applications of the formulas used for percentages in general).  For our problem this is:

Divide both sides by , but leave the fractions for the time being:

Solve for :

This is:

Which is the same as:

%, or % when rounded.

This problem requires knowledge of the compound interest formula, .

Where  is the amount of money owed,  is the sum borrowed,  is the yearly interest rate,  is the amount of times the interest is compounded per year, and  is the number of years.  We know that the student borrowed $200,000 compounded annually at a %6 interest rate, therefore by plugging in those numbers we find that after she graduates in 4 years she will owe $252,495.

The difference in cost is $8 (40 – 32). The sale percentage can be found by figuring out this question: 8 is what percentage of 40? 8/40 = 0.20, or a 20% discount. You can check this. 40 * 0.20 = 8.

40 – 8 = 32

If the average score was 85, we know that the total points earned by the 5 students must be 85 * 5 or 425 points.  Upon adding two new scores, we know that the formula for the average will be:

(425 + x) / 7 = 88, where x stands for the combined points earened by the two new students.

Solve for x: 425 + x = 616; x = 191

This means that both students must score 191 points total.  If this is the case, we can assume that one student earns the maximum points, i.e. 100.  This will provide the minimum amount that could be earned by the other: 191 – 100 = 91.

Given his waste rate, the baker would waste 22 holes. That is the equivalent 3 ²/₃ bags; however, since that would leave him with a ¹/₃ of a bag, the waste really is 4 bags of holes. He therefore fails to make 4 * 0.5 or $2 on this batch of 22 dozen doughnuts and holes.

The sum cost of housing and tutition is $6199.24. To find the percentage of the loan that equals $6199.24, we can set up the equation:

Percentage = .

We then round the percentage to 77.5%.