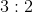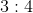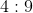The rate is given by amount of probems over time.

To find the amount of problems done in a given amount of time, mulitply the rate by the given amount of time.

We can combine our y terms and cancel our n terms to simplify.

In this rate word problem, we need to find the rates at which Mary and Bejamin frost their respective cupcakes, and then sum their respective rates per hour. In one hour Mary frosts 133 cupcakes. (Note: the question specifies COMPLETELY frosted cupcakes only, so the fractional results here will need to be rounded down to the nearest integer.)  Benjamin frosts 82 cupcakes.

82 + 133=215

This problem states that John can paint a house in  hours. That means in  hour he will be able to paint  of a house.

The problem also states that Jill can paint a house in  hours. This means that in  hour, Jill can paint  of a house.

If they are painting together, you simply add the rate at which the paint separately together to find the rate at which they paint together. This means in  hour, they can paint  of a house. Now to find the time that paint an entire house, we simply invert that fraction, meaning that to paint an entire house together it would take them   of an hour, or .

The general formula for solving these work problems is , where  is the amount of time it takes worker A to finish the job alone and  is the amount of time it would take worker B to finish the job alone.

First, you need to compute the amount of cucumbers used for the salad. A whole salad can be represented as  (like ). Thus, you know:

First, simplify the part of the equation to the left of the equals sign:

Thus, the ratio of lettuce to cucumbers is:

This can be simplified by multiplying both sides by :

We know that the bar could be represented as:

, where  represents . Now, we know that . The remaining apples and soy comprise  of the bar. Now, the apples are one third of that remaining . (This is italicized because it is very important. The common error will be to think that it they are one third of the whole bar.) So, we know apples then are:

Thus, we can compute the soy by subtracting that from the :

Now the ratio of fiber to soy is:

Multiply both factors by  to simplify:

A pie is made up of   crust,  apples,  sugar, and the rest is jelly. What is the ratio of crust to jelly?

To compute this ratio, you must first ascertain how much of the pie is jelly. This is:

Begin by using the common denominator :

So, the ratio of crust to jelly is:

This can be written as the fraction:

, or 

This problem is really an easy fraction division. You should first divide the lemon juice amount by the water amount:

Remember, to divide fractions, you multiply by the reciprocal:

This is the same as saying: 

To find a ratio like this, you simply need to make the fraction that represents the division of the two values by each other. Therefore, we have:

Recall that division of fractions requires you to multiply by the reciprocal:

, 

which is the same as:

This is the same as the ratio:

Begin by manipulating the ratios into whole numbers. Let's begin with the ratio of seniors to freshmen. For every three-eights of a senior, there is one-half of a freshman:

In order to get rid of the denominators, multiply both sides by 8. Then our ratio becomes

or

.

For every three seniors, there are four freshmen. Now let's do freshman to junior:

Multiply both sides by four to get rid of the denominator. Our ratio now becomes

.

For every 8 freshmen, there are 3 juniors. To find our final ratio, let's combine our previous two ratios by finding a common term (in this case freshmen). Because the ratio of seniors to freshmen is 3:4 and the ratio of juniors to freshmen is juniors is 8:3, multiply both sides of the first ratio to make the freshmen terms match.

Our new ratios now look like this:

6 seniors: 8 freshmen

8 freshmen: 3 juniors

Combine the two ratios using the common term:

6 seniors: 8 freshmen: 3 juniors

Take out the middle term:

6 seniors: 3 juniors

Therefore the ratio of seniors to juniors is  making the ratio of juniors to seniors .

First, compute the new number of philosophy books.  This will be .  

The ratio of philosophy books to history books is thus:

This can be reduced by dividing the numerator and the denominator by :

Therefore, the ratio is .