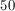GRE Math : Algebra

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1563 : Gre Quantitative Reasoning

Which of the following is equal to $(5^4*5^5)^{20}$ ?

Possible Answers:

$5^{40}$

$25^{29}$

$5^{180}$

$5^{29}$

$25^{180}$

Correct answer:

$5^{180}$

Explanation:

$x^{a} \times x^{b}$ is always equal to $x^{a + b}$ ; therefore, 5 raised to 4 times 5 raised to 5 must equal 5 raised to 9.

$(5^4*5^5)^{20}=(5^{(4+5)})^{20}=(5^9)^{20}$

$(x^{a})^{b}$ is always equal to $x^{(a*b)}$ . Therefore, 5 raised to 9, raised to 20 must equal 5 raised to 180.

$(5^9)^{20}=5^{(9*20)}=5^{180}$

Report an Error

Example Question #21 : Exponential Operations

Which of the following is equal to ((6^7)(5^7))^7 ?

Possible Answers:

$77^{7}$

$210^{7}$

$12^{49}$

$30^{14}$

$30^{49}$

Correct answer:

$30^{49}$

Explanation:

First, multiply inside the parentheses: (6^7)(5^7)=30^7 .

Then raise to the 7th power: $(30^7)^7=30^{49}$ .

Report an Error

Example Question #22 : Exponential Operations

Simplify:

$(6x^{2})^{3}\cdot x^{-7}\cdot 2x^{4}$

Possible Answers:

$12x^{2}$

$432x^{3}$

$6x^{2}$

Correct answer:

$432x^{3}$

Explanation:

Remember, we add exponents when their bases are multiplied, and multiply exponents when one is raised to the power of another. Negative exponents flip to the denominator (presuming they originally appear in the numerator).

$(6x^{2})^{3}\cdot x^{-7}\cdot 2x^{4}$

$=\frac{216x^{6}\cdot 2x^{4}}{x^{7}}$

$=\frac{432x^{10}}{x^{7}}$

$=432x^{3}$

Report an Error

Example Question #23 : Exponential Operations

is a real number such that $y\geq 1$ .

Quantity A: (y^2)(y^4)

Quantity B: y^8

Possible Answers:

Quantity B is greater.

The two quantities are equal.

Quantity A is greater.

The relationship cannot be determined from the information given.

Correct answer:

The relationship cannot be determined from the information given.

Explanation:

(y²)(y⁴) = y²⁺⁴ = y⁶

Plug in two different values for y.

Plug in y = 1: y⁸ = y⁶

Plug in y = 2: y⁸ > y⁶

Since the results differ, the relationship cannot be determined from the information given.

Report an Error

Example Question #22 : Exponents

Evaluate:

$y=\frac{3^{13}-9^{5}}{\left ( \frac{1}{27} \right )^{-3}}$

Possible Answers:

$\dpi{100} \small 78$

$\dpi{100} \small 30$

$\dpi{100} \small 24$

$\dpi{100} \small 27$

$\dpi{100} \small 81$

Correct answer:

$\dpi{100} \small 78$

Explanation:

Can be simplified to:

Capture2

Report an Error

Example Question #474 : Algebra

Simplify the following expression.

$\frac{((x^4)^{-7})}{(x^2*x^4)}$

Possible Answers:

$x^{22}$

$x^{34}$

$\textup{This expression can't be simplified any further}$

$\frac{1}{x^{34}}$

$\frac{1}{x^{22}}$

Correct answer:

$\frac{1}{x^{34}}$

Explanation:

To solve this problem, we must first understand some of the basic concepts of exponents. When multiplying exponents with the same base, one would simply add the powers together with the same base to obtain the result. For example, $x^a*x^b=x^{a+b}$ .

When raising exponents to a certain power, one would simply multiply the power the exponent is being raised to with the exponent itself to obtain the new exponent. The base also gets raised to the same power as it normally would and the new exponent gets put on afterward. For example $({x^a})^{b}=x^{a*b}$ .

Now that we have covered the basic concepts of exponent manipulation, we can now solve the problem. The top part of the expression give to us is $((x^4)^{-7})$ . As we have stated before, when an exponent is raised to a certain power, you simply multiply the power and the exponent together. This results in $x^{4*-7}=x^{-28}$ .

The new expression becomes $\frac{x^{-28}}{(x^2*x^4)}$ .

Solving for the denominator of the equation, we previously stated that when multiplying exponents together with the same base, we simply add the exponents together and keep the same base. Therefore $(x^2*x^4)=x^{2+4}=x^6$ .

The new expression becomes $\frac{x^{-28}}{x^6}$ , however $x^{-28}=\frac{1}{x^{28}}$ , therefore the expression becomes $\frac{1}{x^{28}*x^{6}}=\frac{1}{x^{34}}$ .

Report an Error

Example Question #1155 : Algebra

$\dpi{100} \small \frac{4 }{x} = \frac{2}{25}$

Find x.

Possible Answers:

$\dpi{100} \small \frac{25}{8}$

$\dpi{100} \small \frac{8}{25}$

$\dpi{100} \small 0.25$

$\dpi{100} \small 50$

None

Correct answer:

$\dpi{100} \small 50$

Explanation:

Cross multiply:

$\dpi{100} \small 4 \times 25 = 2x$

$\dpi{100} \small 100 = 2x$

$\dpi{100} \small x = 50$

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

The numerator of a fraction is the sum of 4 and 5 times the denominator. If you divide the fraction by 2, the numerator is 3 times the denominator. Find the simplified version of the fraction.

Possible Answers:

$\frac{1}{3}$

$\frac{1}{2}$

Correct answer:

Explanation:

Let numerator = N and denominator = D.

According to the first statement,

N = (D x 5) + 4.

According to the second statement, N / 2 = 3 * D.

Let's multiply the second equation by –2 and add itthe first equation:

–N = –6D

+[N = (D x 5) + 4]

–6D + (D x 5) + 4 = 0

–1D + 4 = 0

D = 4

Thus, N = 24.

Therefore, N/D = 24/4 = 6.

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

If $\frac{(x-7)}{2x} = \frac{5}{9}$ , what is the value of ?

Possible Answers:

$-\frac{35}{13}$

$\frac{73}{9}$

Correct answer:

Explanation:

Start by cross multiplying to get the equation

$5\cdot2x=(x-7)\cdot 9$

10x = 9x-63 .

Then simplify by subtracting from each side to get the solution,

x = -63 .

Report an Error

Example Question #1575 : Gre Quantitative Reasoning

If $\frac{x}{4} = 15$ , then what is $\frac{3x}{5} - 36$ equal to?

Possible Answers:

Correct answer:

Explanation:

We start by solving for x in $\frac{x}{4} = 15$ by multiplying 4 and 15, which gives us x=60 .

Then substituting 60 for x in,

$\frac{3x}{5} - 36$ gives us

$\frac{180}{5} - 36=36-36=0$ which equals 0.

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Boston, Reading Tutors in Chicago, SAT Tutors in Philadelphia, Algebra Tutors in Philadelphia, Math Tutors in San Diego, Statistics Tutors in Philadelphia, Algebra Tutors in San Diego, Statistics Tutors in New York City, ACT Tutors in New York City, Chemistry Tutors in Phoenix

Popular Courses & Classes

MCAT Courses & Classes in New York City, ACT Courses & Classes in Miami, Spanish Courses & Classes in Boston, MCAT Courses & Classes in Los Angeles, ACT Courses & Classes in New York City, LSAT Courses & Classes in Los Angeles, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in Denver, ACT Courses & Classes in Denver, MCAT Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in Dallas Fort Worth, SAT Test Prep in Miami, ISEE Test Prep in Seattle, SSAT Test Prep in Seattle, MCAT Test Prep in Washington DC, MCAT Test Prep in Chicago, LSAT Test Prep in Miami, MCAT Test Prep in Los Angeles, SSAT Test Prep in Houston, GRE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Algebra

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1563 : Gre Quantitative Reasoning

Example Question #21 : Exponential Operations

Example Question #22 : Exponential Operations

Example Question #23 : Exponential Operations

Example Question #22 : Exponents

Example Question #474 : Algebra

Example Question #1155 : Algebra

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #1575 : Gre Quantitative Reasoning

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details